1 chiếc xà ko đồng chất có chiều dài l=8m , khối lượng 120kg được tì vào 2 đầu AB lên bức tường .Trọng tâm của xà cách A 1 khoảng AG=3m .Hãy xác định lực đỡ của tường lên đầu xà???
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
26 tháng 5 2019
Vì hai bức tường cố định nên khoảng cách giữa chúng không đổi. Khi nhiệt độ tăng thì thanh xà nở dài thêm một đoạn ∆ l = 1,2 mm. Do đó, thanh xà tác dụng lên hai bức tường một lực có cường độ tính theo định luật Húc :
VT
15 tháng 12 2019
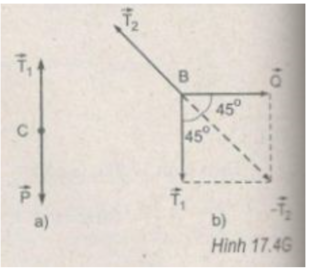
Điểm C đứng cân bầng (H.17.4Ga), nên :
T 1 = P = 40 N
Thanh chống đứng cân bằng (H. 17.4Gb),
ba lực T 1 → , T 2 → và Q → đồng quy ở B. Từ tam giác lực, ta có :
Q = T 1 = P = 40 N
T 2 = T 1 2 = 56,4 ≈ 56 N.
Chú ý: Do tường không có ma sát nên xích phải có ma sát mới giữ được thanh chống, vì vậy T 2 phải lớn hơn T 1
LB
6 tháng 1
Giải:
- Áp dụng công thức tính trọng lượng: \(P=10.m\)
=> Trọng lượng của thanh sắt là: \(P_{thanh^{_{ }}sắt}\)\(=10.30=300N\)
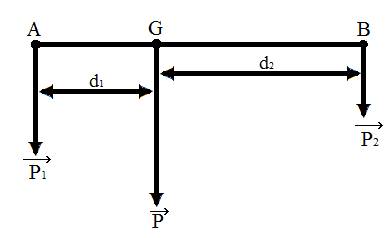
- Có: lực do đầu A của thanh sắt tác dụng lên giá đỡ là: \(P_1=200N\)
=> Lực do đầu B của thanh sắt tác dụng lên giá đỡ là: \(P_2=P-P_1=300-200=100N\)
- Theo quy tắc hợp hai lực song song cùng chiều, ta có:\(\dfrac{P_1}{P_2}=\dfrac{GB}{GA}\Leftrightarrow\dfrac{GB}{GA}=\dfrac{300}{100}=3\Rightarrow3.GB-GB=0\left(1\right)\)
- Có \(GA+GB=AB=3m\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\), ta có hệ sau: \(\left\{{}\begin{matrix}3GB-GB=0\\GA+GB=3m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}GA=0,75m\\GB=2,25m\end{matrix}\right.\)
- Vậy trọng tâm G của thanh cách đầu A một đoạn 0,75m; cách đầu B một đoạn 2,25m.
ĐÂY LÀ VẬT LI MÀ
Bài làm :
Trọng lượng của xà bằng: P = 10.120 = 1200 (N)
Xà chịu tác dụng của 3 lực FA, FB, P
Để tính FA ta coi xà là một đòn bẩy có điểm tựa tại B. Để xà đứng yên ta có:
FA.AB=P.BG=FA =P.\(\frac{GB}{AB}\)=1200.\(\frac{5}{8}\)=750(N)
Để tính FB ta coi xà là một đòn bẩy có điểm tựa tại A xà đứng yên khi:
FB.AB = P.GA = FB =P.\(\frac{GA}{AB}\)=1200.\(\frac{3}{8}\)=450(N)
Vậy lực đỡ của bức tường đầu A là 750 (N), của bức tường đầu B là 450 (N).
Hay thì k
Lưu ý : tìm GB= AB-AG