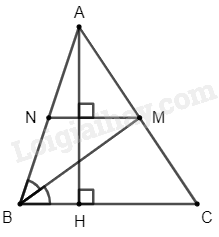
Cho tam giác ABC nhọn có AH vuông với BC .Vẽ tia phân giác của B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH cắt AB tại N.
a.C/m BCMN là hình thang.
b. C/m BN =MN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
\(NM \bot AH\) (gt)
\(BC \bot AH\) (gt)
Suy ra \(NM\) // \(BC\)
Suy ra \(BNMC\) là hình thang
b) Vì \(NM\) // \(BC\) (cmt)
Suy ra \(\widehat {{\rm{NMB}}} = \widehat {{\rm{MBC}}}\) (so le trong)
Mà \(\widehat {{\rm{MBN}}} = \widehat {{\rm{MBC}}}\) (do \(MB\) là phân giác)
Suy ra \(\widehat {{\rm{MBN}}} = \widehat {{\rm{NMB}}}\)
Suy ra \(\Delta MNB\) cân tại \(N\)
Suy ra \(BN = NM\)

\(a,\left\{{}\begin{matrix}MN\perp AH\\BC\perp AH\end{matrix}\right.\Rightarrow MN//BC\Rightarrow BCMN\) là hthang
\(b,MN//BC\Rightarrow\widehat{CBM}=\widehat{BMN}\\ Mà.\widehat{NBM}=\widehat{CBM}\left(t/c.phân.giác\right)\\ \Rightarrow\widehat{BMN}=\widehat{NBM}\)
Do đó tam giác BMN cân tại N nên \(BM=MN\)

a: Xét ΔMHC và ΔMKC có
CH=CK
\(\widehat{HCM}=\widehat{KCM}\)
CM chung
Do đó: ΔMHC=ΔMKC
Suy ra: MH=MK

a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm

a: góc NED+góc NCD=180 độ
=>NEDC nội tiếp
b: ΔAHB vuôg tại H có HM vuông góc AB
nên AM*AB=AH^2
ΔAHC vuông tại H có HN vuông góc AC
nên AN*AC=AH^2
=>AM*AB=AN*AC
a) Gọi giao điểm của NM và AH là F. Khi đó theo đề bài ta có:^MFA = ^CHF (=90o). Mà hai góc này ở vị trí đồng vị nên MN // BC.
Do đó BCMN là hình thang.
b)Đề có sai không? Nếu vẽ hình ra AB < AC thì thấy MN > BN
P/s: Không chắc ở câu a