Cho hình thang cân ABCD (AD // BC, AD < BC). Gọi O là giao điểm của hai đường chéo. Gọi M là trung điểm của BC. Chứng minh OM vuông góc AD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GH
22 tháng 6 2023
2)
Có: \(\left\{{}\begin{matrix}AB=AD\left(gt\right)\\AD=BC\left(2.cạnh.bên.hình.thang.cân\right)\end{matrix}\right.\)
\(\Rightarrow AB=BC\Rightarrow\Delta ABC.cân.tại.B\)
Mà AB // ED (gt)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\left(so.le.trong\right)\)
\(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
=> CA là tia phân giác của góc C.
11 tháng 8 2020
( Hình tự vẽ nha bạn )
giải
Ta có: ∠(ADC) = ∠(BCD) (gt)
⇒ ∠(ODC) = ∠(OCD)
⇒ΔOCD cân tại O (dhnb tam giác cân)
⇒ OC = OD
OB + BC = OA + AD
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ΔADC và. ΔBCD:
AD = BC (hình thang ABCD cân )
AC = BD (hình thang ABCD cân)
CD chung
Do đó ΔADC và ΔBCD (c.c.c)
⇒ ∠ADC= ∠BCD (2 góc tương ứng)
⇒ΔEDC cân tại E (dhnb tam giác cân)
⇒ EC = ED nên E thuộc đường trung trực CD
OC = OD nên O thuộc đường trung trực CD
E ≠ O. Vậy OE là đường trung trực của CD.
Ta có: BD= AC (tính chất hình thang cân)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
OA = OB (chứng minh trên ) nên O thuộc đường trung trực của AB
E ≠ O. Vậy OE là đường trung trực của AB.
8 tháng 8 2016
Tham khảo nha
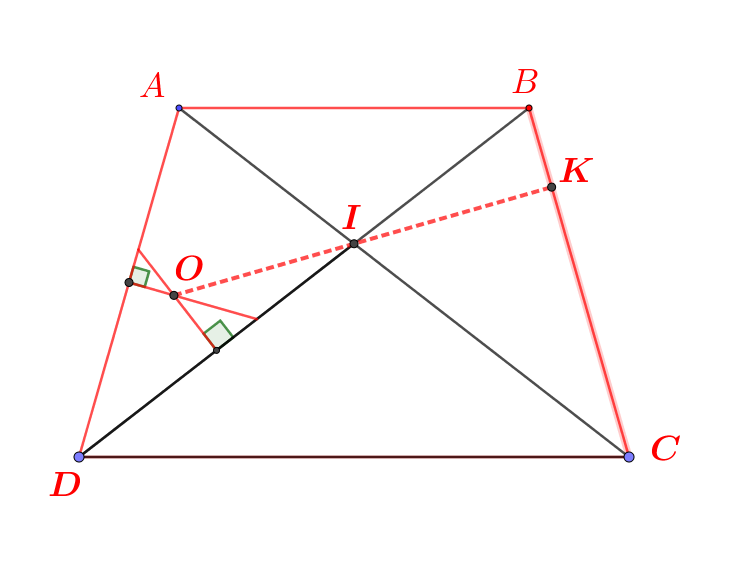
Xét tứ giác AEDO có góc A và D vuông=> AEDO nội tiếp đường tròn
=>góc AED+góc AOD=180(2 góc đối nhau) (1)
góc B chắn cung AD=> góc AOD=2*góc ABD mà tam giác ABI cân tại I nên góc ABD = góc BAC = 1/2 góc AOD=>góc ABD+BAC=AOD. Vì góc AID kề bù với góc AIB=> gócAID+góc AIB=180=AIB+ABD+BAC=AIB+AOD=>góc AID= góc AOD
từ (1)=> góc AED+góc AID=180(đpcm)
Xét ΔACD và ΔDBA có
AC=DB
AD chung
CD=BA
Do đó: ΔACD=ΔDBA
Suy ra: \(\widehat{CAD}=\widehat{BDA}\)
hay \(\widehat{OAD}=\widehat{ODA}\)
Xét ΔOAD có \(\widehat{OAD}=\widehat{ODA}\)
nên ΔOAD cân tại O
Suy ra: OD=OA
hay O nằm trên đường trung trực của DA(1)
Xét ΔABM và ΔDCM có
AB=DC
\(\widehat{ABM}=\widehat{DCM}\)
BM=CM
Do đó: ΔABM=ΔDCM
Suy ra: MA=MD
hay M nằm trên đường trung trực của AD(2)
Từ (1)và (2) suy ra OM là đường trung trực của AD
hay OM\(\perp\)AD
Thanks you so much!