Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Để tính vận tốc trung bình, ta sử dụng công thức:
Vận tốc trung bình = Quãng đường / Thời gian
a) Trong lần bơi đầu tiên theo chiều dài bể bơi:
Quãng đường: 50m Thời gian: 20s
Vận tốc trung bình = 50m / 20s = 2.5 m/s
Vậy vận tốc trung bình trong lần bơi đầu tiên theo chiều dài bể bơi là 2.5 m/s.
b) Trong lần bơi về:
Quãng đường: 50m Thời gian: 22s
Vận tốc trung bình = 50m / 22s ≈ 2.27 m/s
Vậy vận tốc trung bình trong lần bơi về là khoảng 2.27 m/s.
c) Trong suốt quãng đường bơi đi và về:
Quãng đường đi + quãng đường về = 50m + 50m = 100m Thời gian đi + thời gian về = 20s + 22s = 42s
Vận tốc trung bình = 100m / 42s ≈ 2.38 m/s
Chọn B.
*Tốc độ trung bình tính theo công thức:
v tb = Quãng đường đi được Thời gian đi quãng đường đó = s t
Lần đi: v1 = 50/40 = 1,25 (m/s)
Lần về: v2 = 50/42 = 1,19 (m/s)
Cả đi và về:
v 3 = 2 . 50 40 + 42 = 1 , 22 ( m / s ) ⇒ v 1 + v 2 + 2 v 3 = 4 , 88 ( m / s ) .
Chọn đáp án A
? Lời giải:
+ Giả sử người này bơi từ A đến B rồi quay lại về A. Chọn chiều dương từ A đến B, gốc tọa độ và gốc thời gian tại A. Trong suốt quãng đường đi và về, độ dời: Δx = x2 – x1
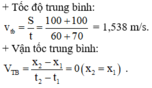
ĐS: a.&space;&&space;\\&space;\bar{v}=2,5&space;(m/s)&&space;\end{matrix})
; b.&space;&&space;\\&space;\bar{v}=2(m/s)&&space;\end{matrix}\right.)
; c.&space;&&space;\\&space;\bar{v}\approx&space;2,2&space;(m/s)&&space;\end{matrix}\right.)
Tham khảo!
Theo đề bài AB=50m (A là vị trí xuất phát). Chọn A là gốc tọa độ, chiều dương của trục tọa độ hướng từ A đến B
a) Khi người đó bơi từ A đến B thì: \(s_1=50m,\Delta x_1=+50m\)
Tốc độ trung bình: \(\overrightarrow{v_{tb1}}=\frac{S_1}{\Delta t_1}=2,5m/s\)
Vận tốc trung bình:\(v_{tb1}=\frac{\Delta x_1}{\Delta t_1}=+2,5m/s\) và hướng của vectơ \(\overrightarrow{v_{tb}}\) từ A đến B.
b) Khi người đó bơi quay trở lại: \(S_2=50,\Delta x_2=-50m\)
Tốc độ trung bình : \(\overrightarrow{v_{tb2}}=\frac{S_2}{\Delta t_2}=2,27m/s\)
Vận tốc trung bình:\(v_{tb2}=\frac{\Delta x_2}{\Delta t_2}=-2,27m/s\) hướng của vectơ \(\overrightarrow{v_{tb}}\) từ B đến A
c) Nếu xét cả quá trình bơi đi và bơi về:
\(S_3=100m\)
độ rời \(\Delta x_3=\Delta x_1+\Delta x_2=0\)
Tốc độ trung bình: \(\overrightarrow{v_{tb3}}=\frac{S_3}{\Delta t_3}=...\)
Vận tốc trung bình:\(v_{tb3}=\frac{\Delta x_3}{\Delta t_3}=...\)