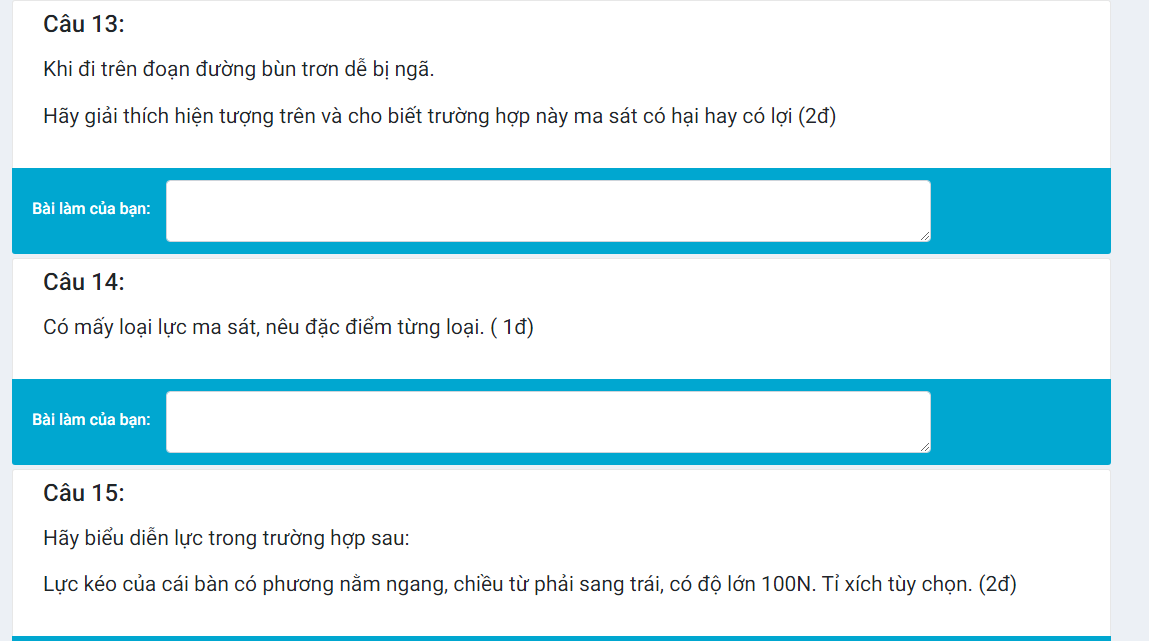
Làm giúp mình bài 10 đi ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{3}{2}-tana\cdot cos^2a\)
\(=\dfrac{3}{2}-\dfrac{sina}{cosa}\cdot cos^2a\)
\(=\dfrac{3}{2}-sina\cdot cosa\)
\(=\dfrac{3}{2}-\dfrac{1}{2}sin2a\)
\(0^0< a< 90^0\)
=>\(0< =2a< =180^0\)
=>\(sin2a\in\left[-1;1\right]\)
\(-1< =sin2a< =1\)
=>\(\dfrac{1}{2}>=-\dfrac{1}{2}sin2a>=-\dfrac{1}{2}\)
=>\(\dfrac{7}{2}>=-\dfrac{1}{2}sin2a+3>=\dfrac{5}{2}\)
=>\(\dfrac{5}{2}< =y< =\dfrac{7}{2}\)
\(y_{min}=\dfrac{5}{2}\) khi sin2a=1
=>\(2a=\dfrac{\Omega}{2}+k2\Omega\)
=>\(a=\dfrac{\Omega}{4}+k\Omega\)
mà 0<a<90
nên a=45

11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)

mình ko bt
mình moi đi cách ly về nó mà cô giao ko tin'
Xin lỗi em nhé, do theo quy tắc thì các câu hỏi liên quan đến thi cử và kiểm tra thì sau 1 h kể từ khi đăng bài mn mới dc làm. Nên anh mong em có thể chịu lùi bc này để ôn tốt hơn nha



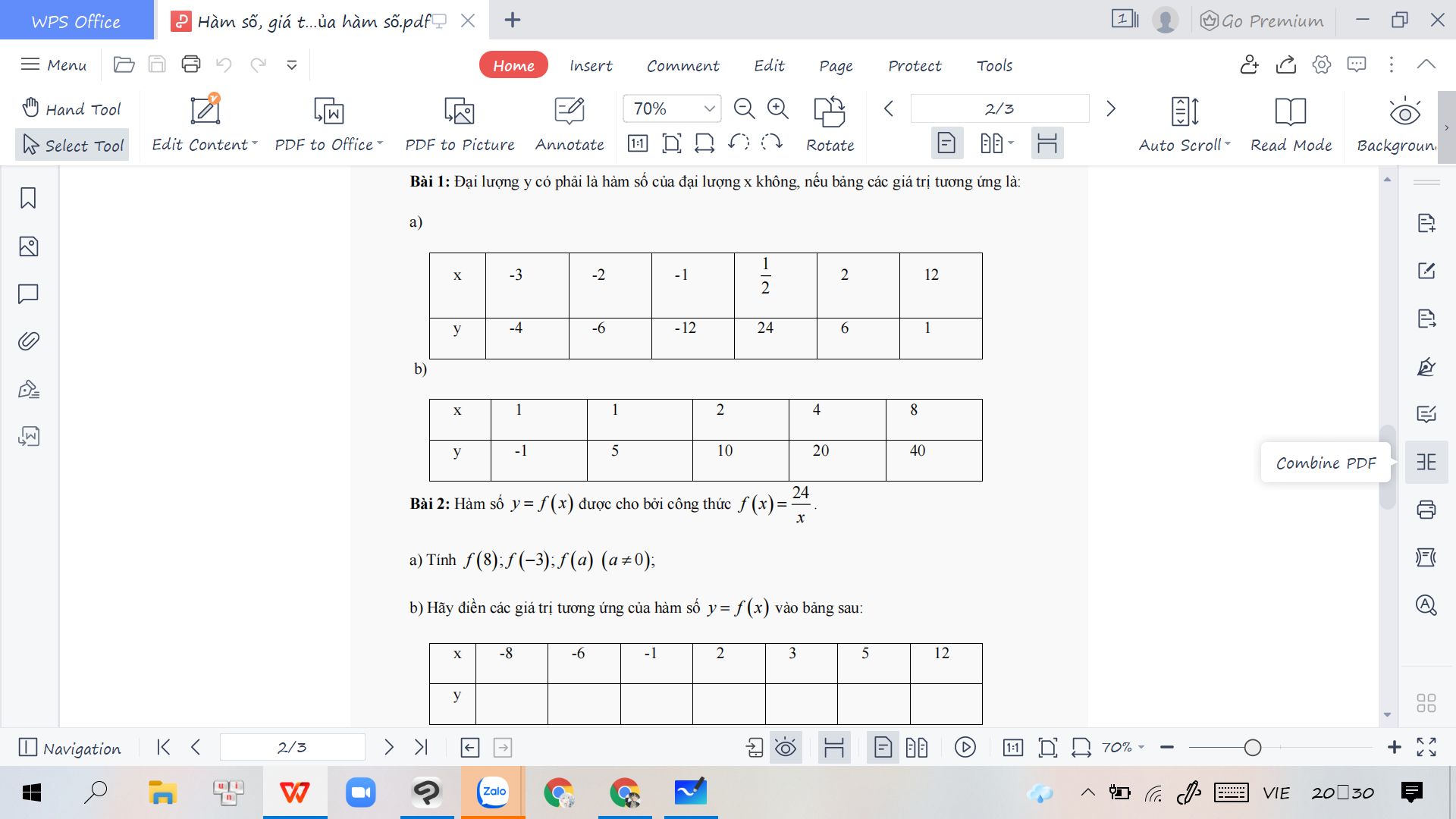
 Mọi người ơi giúp 2 bài giải có lời giải chi tiết đi ạ ảnh dưới là cách làm mẫu làm ơn giúp mình vì mình đang cần gấp!
Mọi người ơi giúp 2 bài giải có lời giải chi tiết đi ạ ảnh dưới là cách làm mẫu làm ơn giúp mình vì mình đang cần gấp!