Cho a,b,n ∈ N*. Biết rằng với mọi số tự nhiên k khác b ta đều có kn - a ⋮ k - b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: a^n=1
=>a^n=1^n
=>a=1
b: x^50=x
=>x^50-x=0
=>x(x^49-1)=0
=>x=0 hoặc x^49-1=0
=>x=0 hoặc x^49=1
=>x=0 hoặc x=1

svtkvtm bài giải đây nha
Xét k > b
Ta có:
\(\left\{{}\begin{matrix}k^n-a⋮k-b\\k^n-b^n⋮k-b\end{matrix}\right.\)
\(\Rightarrow b^n-a⋮k-b\)
Mà theo đề bài là với mọi k khác b nên sẽ tồn tại số k sao cho
\(\left\{{}\begin{matrix}k-b>b^n-a\left(b^n-a>0\right)\\k-b< b^n-a\left(b^n-a< 0\right)\end{matrix}\right.\)
Điều này chỉ xảy ra khi \(b^n-a=0\)hay \(a=b^n\)

a, Với n = 0 => x 0 = 1 ⇒ ∀ x ∈ N
Với n ≠ 0 => x n = 1 ⇒ x = 1
b, x n = 0 => x = 0
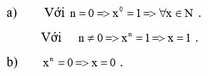
CMR: a=bn