Tìm số tự nhiên n lớn nhất sao cho 29n là ước của 2003!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
2
9 tháng 2 2018
Ta có: \(29^n\varepsilon U\left(2003\right)\Leftrightarrow29^n\le2003\Rightarrow n< 3\)mà\(n\varepsilon N\Rightarrow n\varepsilon\left\{0;1;2\right\}\Rightarrow29^n\varepsilon\left\{1,29,841\right\}\left(1\right)\)
Lại có:\(2003⋮29^n\left(2\right)\)
Từ (1) và (2) => n = 0
SL
0
TN
23 tháng 12 2021
a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
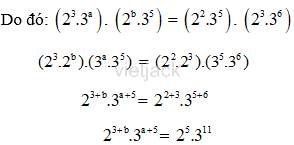
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
DN
11 tháng 11 2022
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y=
Mà xy =
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6
1 tháng 1 2022
a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)
11 tháng 1 2022
a: \(\Leftrightarrow n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)
TM
15 tháng 10 2017
a=1.2.3.4.5.6.7.8.9.10.
=2^8.3^4.5^2.7
=(2^4.3^2.5)^2.7
Vậy n=2^4.3^2.5=720
KZ
3
29 tháng 7 2016
- Gọi d là ước chung lớn nhất của n và n + 2
=> n chia hết d và n + 2 chia hết d
=> ( n + 2 ) - n chia hết d
=> 2 chia hết d
=> d = 1 hoặc 2
Nếu n lẻ => d = 1
Nếu n chẵn => d = 2
Vậy ước chung lớn nhất của n và n + 2 là 1 hoặc 2
Ta có : Nếu ước chung lớn nhất của n và n + 2 = 1
thì bội chung nhỏ nhất của n và n +2 = n(n+2)
Nếu ước chung lớn nhất của n và n +2 là 2
thì bội chung nhỏ nhất của n và n +2 = n(n+2) : 2
Làm như thế này có đúng không vậy ?
1 tháng 6 2016
câu trả lời là mới hok lp 5 sang năm lên lp 6 :)
1 tháng 6 2016
Gọi 2 số đó là a và b, ƯCLN(a,b)=d
=>a=da'
b=db'
(a',b')=1
BCNN(a,b)=da'b'
Tổng ƯCLN và BCNN là d+da'b'=d(a'b'+1)=126
126 phân tích ra thừa số nguyên tố là 2.32.7
Do đó d=2 hoặc a'b'+1=2
Nếu d=2 thì a'b'+1=126:2=63
a'b'=62. Giả sử a>b thì a'>b'
TH1: a'=31, b'=2 =>a=31.2=62, b=2.2=4. a-b=58
TH2 a'=62, b'=1 =>a=62.2=124, b=2. a-b=122.
Hiệu nhỏ nhất nếu d=2 là 58
Tiếp theo ta xét
a'b'+1=2
a'b=1
=>a'=b'=1
Khi đó d=126:2=63
Ta có a=63, b=63
a-b=0
Tuy nhiên đề bài yêu cầu tìm hiệu dương mà số 0 ko dương cũng ko âm
Vậy 2 số cần tìm là 62 và 4
Từ 1 tới 2003, số lượng số hạng chia hết cho 29 là:
\(\frac{\left(2001-29\right)}{29}+1=69\). Vậy 2003❗ chia hết cho \(29^{69}\)
Vậy n lớn nhất bằng 69 thì \(29^n\) là ước của 2003❕
Có 71 cơ bn ạ. Mk bt nhưng k bt trình bày ntn thôi.