Cho tam giác BCD vuông tại B, BC<BD. Vẽ đường cao BH.
a) Chứng mình rằng tầm giác BCD đồng dạng với tâm giác HCB. Từ đó suy ra CH.CD=CB².
b) Cho BC=15cm, BD=20cm. Tính độ dài các đoạn thẳng CD,CH.
Nếu vẽ hình được thì mình cảm ơn 🥰🥰🥰
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: AD=AC(gt)
mà A nằm giữa hai điểm C và D(gt)
nên A là trung điểm của CD
Xét ΔBCD có
BA là đường trung tuyến ứng với cạnh CD(A là trung điểm của CD_
BA là đường cao ứng với cạnh CD(BA⊥CA, D∈CA)
Do đó: ΔBCD cân tại B(Định lí tam giác cân)
Sửa đề: Góc B = 30 độ
----------------------------------------
a) Ta có: \(\widehat{BAC}+\widehat{BAD}=180^0\) (kề bù)
\(\Rightarrow\widehat{BAD}=180^0-\widehat{BAC}=180^0-90^0=90^0\)
Xét ΔBAD và ΔBAC ta có:
AD = AC (GT)
Góc BAD = Góc BAC (= 900)
AB: canhj chung
=> ΔBAD = ΔBAC (c - g - c)
=> Góc C = Góc D (2 góc tương ứng)
=> Tam giác BDC cân tại B (1)
ΔABC vuông tại A
\(\Rightarrow\widehat{ABC}+\widehat{C}=90^0\)
\(\Rightarrow\widehat{C}=90^0-\widehat{ABC}=90^0-30^0=60^0\left(2\right)\)
Từ (1) và (2) => Tam giác BDC đều
b) Tam giác BDC đều
=> BC = CD
Mà: CD = 2. AC
=> BC = 2.AC

a: Xét ΔCBA vuông tại B và ΔCHA vuông tại H có
CA chung
\(\widehat{BCA}=\widehat{HCA}\)
Do đó: ΔCBA=ΔCHA
Suy ra: BA=HA
b: Xét ΔBAE vuông tại B và ΔHAD vuông tại H có
BA=HA
\(\widehat{BAE}=\widehat{HAD}\)
Do đó: ΔBAE=ΔHAD

a) Chứng minh được tam giác ABC = tam giác A.BD (c-g-c), từ đó suy ra được tam giác BCD đều
b) Dùng kết quả câu a, ta có BC = CD = 2AC

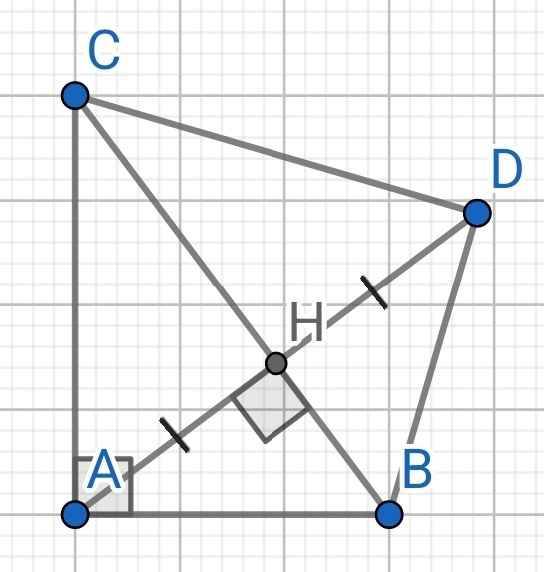 a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
AH = DH (gt)
BH là cạnh chung
⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)
b) Sửa đề: Chứng minh ∠BDC = 90⁰
Do ∆ABH = ∆DBH (cmt)
⇒ ∠ABH = ∠DBH (hai góc tương ứng)
AB = BD (hai cạnh tương ứng)
Do ∠ABH = ∠DBH (cmt)
⇒ ∠ABC = ∠DBC
Xét ∆ABC và ∆DBC có:
AB = BD (cmt)
∠ABC = ∠DBC (cmt)
BC là cạnh chung
⇒ ∆ABC = ∆DBC (c-g-c)
⇒ ∠BAC = ∠BDC = 90⁰
Vậy ∠BDC = 90⁰

1) Đề sai chỗ này nhé:\(CH\times CD=CB^2\) chứ không phải là \(CH\times CD=CB\) đâu bạn!
GIẢI
Xét \(\Delta BCD\)và \(\Delta HCB\) có:
\(\widehat{B}=\widehat{H}=90^o\)
\(\widehat{C}\)là góc chung
\(\Rightarrow\Delta BCD\) đồng dạng với \(\Delta HCB\left(g.g\right)\)
Vì \(\Delta HCB\) đồng dạng với \(\Delta BCD\) ( chứng minh trên )
\(\Rightarrow\frac{HC}{BC}=\frac{BC}{CD}\Rightarrow HC.CD=BC^2\)
\(\Rightarrowđpcm\)
a) Xét \(\Delta BCD\) và \(\Delta HCB\) có
\(\widehat{BCD}:chung;\widehat{CBD}=\widehat{CHB}=90^o\)
=> \(\Delta BCD\) ~ \(\Delta HCB\)
=>\(\frac{BC}{HC}=\frac{CD}{BC}=BC^2=CH.CD\)
b( Xét \(\Delta BCD\) vuông tại B có "
\(CD^2=BC^2+BD^2=15^2+20^2=625\Rightarrow CD=25cm\)
Có \(\frac{BC}{HC}=\frac{CD}{BC}=BC^2=CH.CD\Rightarrow CH=9cm\)
E tự vẽ hình ạ🥴