Giải hộ em câu này. Câu hỏi dưới bình luận 👇
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{n!}{\left(n-3\right)!}=\frac{72.n!}{\left(n-1\right)!}\Leftrightarrow\left(n-1\right)\left(n-2\right)=72\)
\(\Leftrightarrow n^2-3n-70=0\Rightarrow\left[{}\begin{matrix}n=10\\n=-7\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\sum\limits^n_{k=0}C_n^k=\sum\limits^{10}_{k=0}C_{10}^k\)
Xét khai triển:
\(\left(x+1\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k.x^k\)
Thay \(x=1\) ta được: \(2^{10}=\sum\limits^{10}_{k=0}C_{10}^k\)
Vậy kết quả bài toán: \(2^{10}=1024\)

Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}< >-\dfrac{1}{m}\)
=>\(m^2\ne-3\)(luôn đúng)
Ta có: \(\left\{{}\begin{matrix}mx-y=2\\3x+my=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\left(mx-2\right)=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m^2x-2m=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=m\cdot\dfrac{5m}{m^2+3}-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=\dfrac{5m^2-2m^2-6}{m^2+3}=\dfrac{3m^2-6}{m^2+3}\end{matrix}\right.\)
\(\left(x+y\right)\cdot\left(m^2+3\right)+8=0\)
=>\(\dfrac{5m+3m^2-6}{m^2+3}\cdot\left(m^2+3\right)+8=0\)
=>\(3m^2+5m-6+8=0\)
=>\(3m^2+5m+2=0\)
=>(m+1)(3m+2)=0
=>\(\left[{}\begin{matrix}m=-1\\m=-\dfrac{2}{3}\end{matrix}\right.\)

a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp

d: \(=\dfrac{-9\sqrt{3}-6\sqrt{2}}{19}-\dfrac{\sqrt{3}}{5}\)
\(=\dfrac{-64\sqrt{3}-30\sqrt{2}}{95}\)
b: \(=\dfrac{37\left(7-2\sqrt{3}\right)}{49-12}=7-2\sqrt{3}\)

a: Ta có: \(P=A\cdot B\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\cdot\dfrac{\sqrt{x}+6}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}+6}{\sqrt{x}+1}\)
Để P nguyên thì \(\sqrt{x}+1\in\left\{1;5\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;4\right\}\)
hay \(x\in\left\{0;16\right\}\)
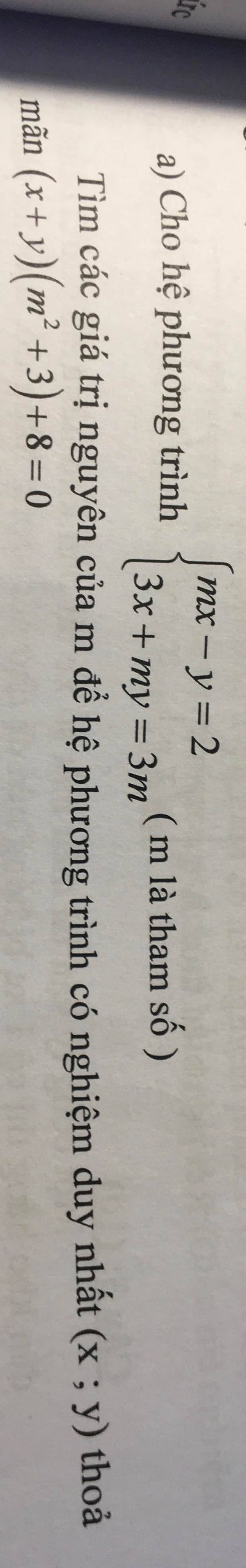
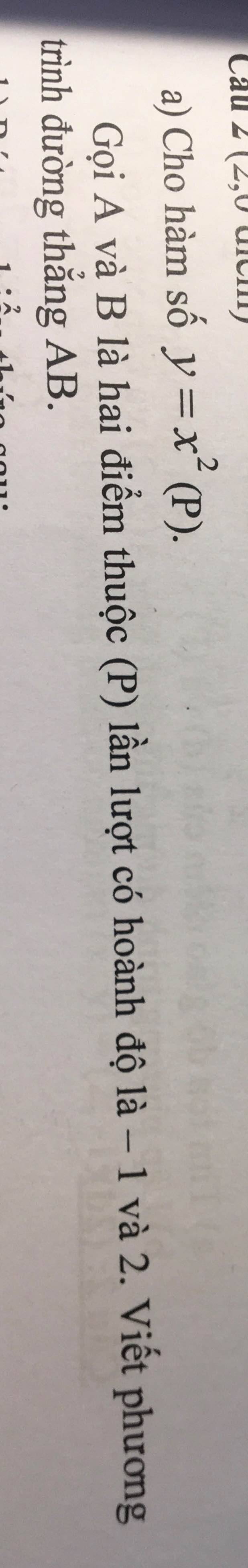







Phương trình hoành độ giao điểm của đường thẳng và đồ thị hàm số
Vậy đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt \(A\left(0;-2\right),B\left(-1,-3\right)\)
Đáp án : B