Cho \(\Delta ABC\) vuông tại A, đường cao AH, AB = 20cm, HC = 9cm. Tính độ dài AH và BC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
16 tháng 6 2019
Áp dụng hệ thực giữa cạnh và đường cao trong tam giác vuông có:
\(AH^2=AB.BH\)
\(\Leftrightarrow20^2=BH\left(BH+9\right)\)
\(\Leftrightarrow BH^2+94H-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
Lại có: \(BC=BH+HC=16+9=25\left(cm\right)\)
\(\Rightarrow AH^2=BH.CH=16.9=12^2\)
\(\Rightarrow AH=12\left(cm\right)\)
16 tháng 6 2019
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
AB^2=BH.BC
<=>20^2=BH.(BH + 9)
<=>BH^2 + 9BH-400=0
=> BH=16cm
Mà BC=BH + HC=16 + 9=25cm
AH^2 = BH.HC = 16.9 = 12^2
suy ra AH = 12cm.
Vậy AH=12cm.
HT
0
TP
2
3 tháng 9 2016
Áp dụng hệ thực giữa cạnh và đường cao trong tam giác vuông có:
\(AH^2=AB.BH\)
\(\Leftrightarrow20^2=BH\left(BH+9\right)\)
\(\Leftrightarrow BH^2+94H-400=0\)
\(\Rightarrow BH=16\left(cm\right)\)
Lại có: \(BC=BH+HC=16+9=25\left(cm\right)\)
\(\Rightarrow AH^2=BH.CH=16.9=12^2\)
\(\Rightarrow AH=12\left(cm\right)\)
TL
3
NT
24 tháng 5 2016
Gọi AC=a;BH=b
thì ta có hệ pt \(\sqrt{a^2+20^2}=9+b\)(pytago)
\(\frac{20a}{b+9}=\sqrt{9b}\)(hệ thức lượng trong tam giác vuông)
7 tháng 8 2023
AB^2=BH*BC
=>BH(BH+9)=20^2=400
=>BH^2+9BH-400=0
=>(BH+25)(BH-16)=0
=>BH=16cm
AH=căn BH*CH=12(cm)
14 tháng 5 2023
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔABC vuông tại A có AH vuông góc BC
nên AH^2=HB*HC
c: \(AC=\sqrt{20^2-12^2}=16\left(cm\right)\)
AH=12*16/20=192/20=9,6cm
VD
1
24 tháng 10 2015
v~
ta có \(AB^2=BH.BC=BH.\left(BH+9\right)=BH^2+9BH\)
\(BH^2+9BH-AB^2=0\)
\(\Leftrightarrow BH^2+9BH-20^2=0\Leftrightarrow BH^2+9BH-400=0\)
\(\Leftrightarrow BH^2-16BH+25BH-400=0\)
\(\Leftrightarrow BH\left(BH-16\right)+25\left(BH-16\right)=0\)
\(\Leftrightarrow\left(BH-16\right)\left(BH+25\right)=0\)
=> BH = 16 VÀ BH = -25 ( loại )
=> BH = 16
\(AH=\sqrt{AB^2-BH^2}=\sqrt{20^2-16^2}=12\)
CHỖ NÀO KO HỈU HỎI LẠI MIK NHAN !!!
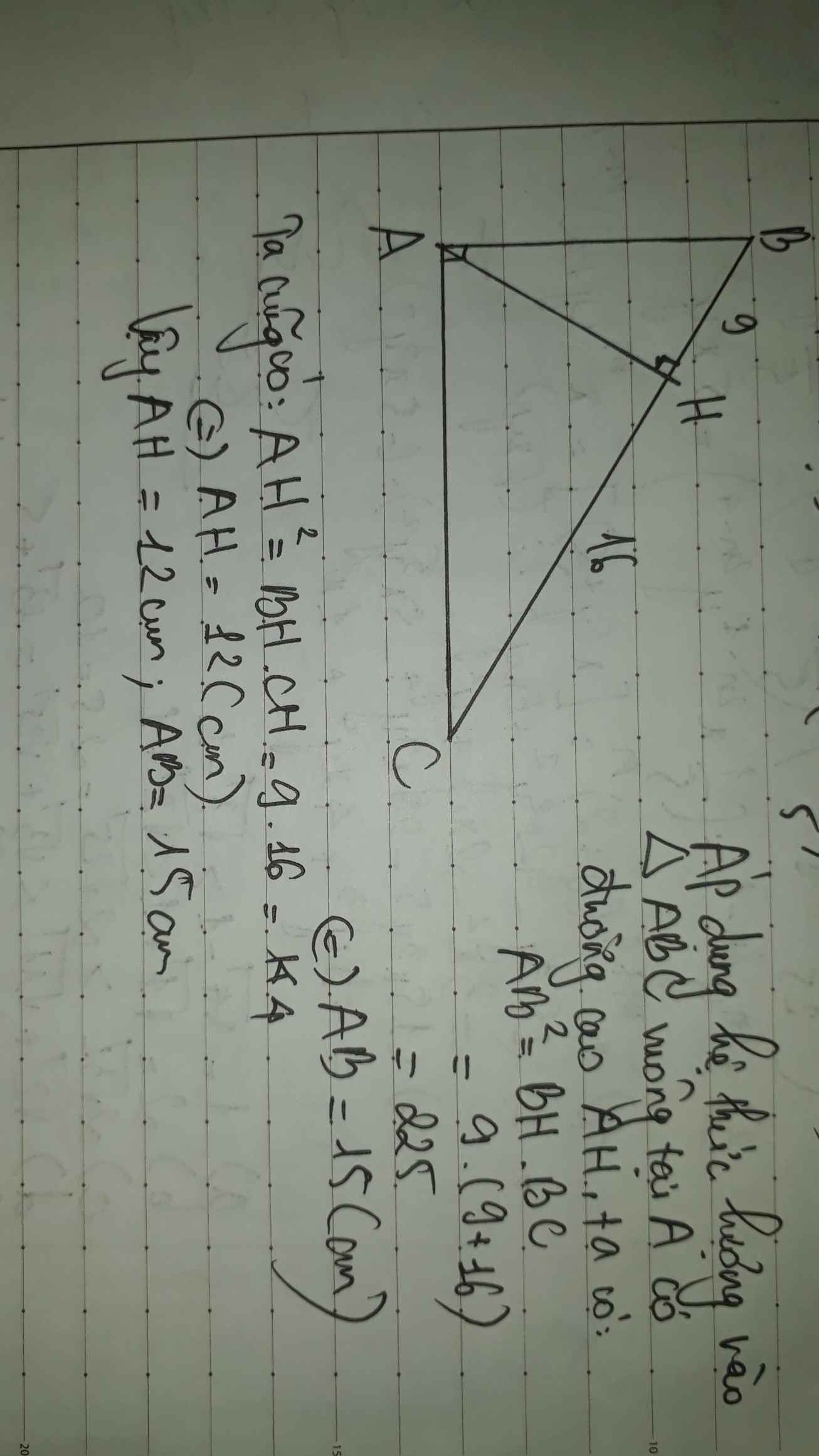
Có \(AB^2=BH.BC=BH\left(BH+HC\right)\)\(\Leftrightarrow20^2=BH^2+9BH\Leftrightarrow BH^2+9BH-400=0\)
\(\Leftrightarrow BH=16cm\)
\(\Rightarrow BC=HC+HB=9+16=25cm\)
\(\Rightarrow AH^2=HB.HC\Leftrightarrow AH=\sqrt{HB.HC}=12cm\)