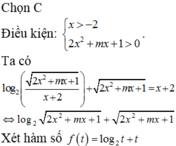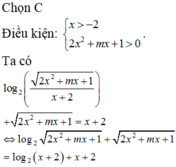có bao nhiêu giá trị nguyên của tham số m để phương trinh \(15^x-5^x-3^x=\dfrac{m}{10}\) có 2 nghiệm thực phân biệt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 11 2023
Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 8 2021
\(\Leftrightarrow\left\{{}\begin{matrix}3.2^xlogx-12logx-2^x+4=0\left(1\right)\\5^x=m\left(2\right)\end{matrix}\right.\) và \(5^x\ge m\) (\(x>0\))
Xét (1):
\(\Leftrightarrow3logx\left(2^x-4\right)-\left(2^x-4\right)=0\)
\(\Leftrightarrow\left(3logx-1\right)\left(2^x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=2\\x_2=\sqrt[3]{10}\end{matrix}\right.\)
\(y=5^x\) đồng biến trên R nên (2) có tối đa 1 nghiệm
Để pt đã cho có đúng 2 nghiệm phân biệt ta có các TH sau:
TH1: (2) vô nghiệm \(\Rightarrow m\le0\) (ko có số nguyên dương nào)
TH2: (2) có nghiệm (khác với 2 nghiệm của (1)), đồng thời giá trị của m khiến cho đúng 1 nghiệm của (1) nằm ngoài miền xác định
(2) có nghiệm \(\Rightarrow m>0\Rightarrow x_3=log_5m\)
Do \(\sqrt[3]{10}>2\) nên bài toán thỏa mãn khi: \(x_1< x_3< x_2\)
\(\Rightarrow2< log_5m< \sqrt[3]{10}\)
\(\Rightarrow25< m< 5^{\sqrt[3]{10}}\) (hơn 32 chút xíu)
\(\Rightarrow\) \(32-26+1\) giá trị nguyên
NH
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 11 2021
Đặt \(\left|x\right|=t\ge0\)
\(\Rightarrow t^2-2t+1-m=0\) (1)
Phương trình (1) là bậc 2 nên có đối đa 2 nghiệm t
Với mỗi giá trị \(t>0\) cho 2 nghiệm x tương ứng nên pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=1-\left(1-m\right)>0\\t_1+t_2=2>0\\t_1t_2=1-m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m< 1\end{matrix}\right.\) \(\Leftrightarrow0< m< 1\)
CM
2 tháng 5 2019
Chọn đáp án D
Phương pháp
Cho ba số a, b, c lập thành CSN thì ta có: b 2 = a c .
Cách giải
Ta có: ( x - 1 ) ( x - 3 ) ( x - m ) = 0
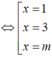
Phương trình đã cho có 3 nghiệm phân biệt
+) Giả sử 1; 3; m lập thành 1 CSN tăng
+) Giả sử m; 1; 3 lập thành 1 CSN tăng
+) Giả sử 1; m; 3 lập thành 1 CSN tăng
Vậy có 3 giá trị m thỏa mãn