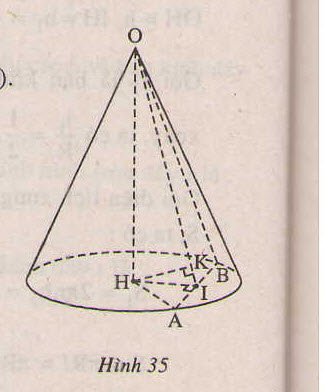
c) Một thiết diện đi qua đỉnh của hình nón và khoảng cách từ tâm của đáy đến mặt phẳng thiết diện là 12cm. Tính diện tích thiết diện đó ?
giúp mình lên diểm hỏi dáp nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 4 2017
Gọi hình nón đã cho có đỉnh là S và H là tâm đường tròn đáy.
Thiết diện đi qua đỉnh S là tam giác SAC (với A và C thuộc đường tròn đáy)
Gọi M là trung điểm của AC.
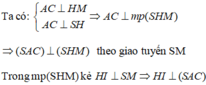
Do đó, d( H; (SAC))= HI = 12
Trong tam giác vuông SHM ta có:
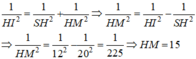
Trong tam giác vuông HAM ta có:
AM2 = HA2 – HM2 = 252 – 152 = 400 nên AM = 20 (cm)
Ta có:
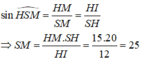
Do đó, diện tích thiết diện SAC là:
HB
26 tháng 4 2017
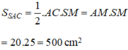
b)-Mặt phẳng (DMN) cắt hình lập phương theo thiết diện MEDNF trong đó ME // ND, FN //DE và chia hình lập phương thành hai khối đa diện (H) và (H’), gọi phần khối lập phương chứa A, B, A’, mặt phẳng (DMN) là (H)
-Chia (H) thành các hình chóp F.DBN, D.ABFMA’ và D.A’EM.
CM
11 tháng 8 2019
Đáp án D.
Giả sử hình nón có đỉnh S, đáy là đường tròn tâm I bán kính r, thiết diện đi qua đỉnh là ∆ S A D cân tại S.
Gọi J là trung điểm của AB, ta có A B ⊥ I J A B ⊥ S I → A B ⊥ S I J → S A B ⊥ S I J
Trong mặt phẳng (SIJ): Kẻ I H ⊥ S J , H ∈ S J
Từ S A B ⊥ ( S I J ) ( S A B ) ∩ ( S I J ) = S J → I H ⊥ S A B → I H = d ( I ; ( S A B ) ) = 24 ( c m ) I H ⊥ S J
1 I H 2 = 1 S I 2 + 1 S J 2 → 1 I J 2 = 1 24 2 - 1 40 2 = 1 900 → I J = 30
→ S J = S I 2 + I J 2 = 50 ( c m )
A B = 2 J A = 2 r 2 - I J 2 = 2 50 2 - 30 2 = 80 ( c m )
Vậy S ∆ S A B = 1 2 S J . A B = 1 2 . 50 . 80 = 2000 ( c m 2 )
CM
3 tháng 1 2019
Đáp án D.
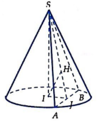
Giả sử hình nón có đỉnh S, đáy là đường tròn tâm I bán kính r, thiết diện đi qua đỉnh là ∆ SAD cân tại S.
Gọi J là trung điểm của AB, ta có
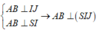
=> (SAB) ⊥ (SIJ)
Trong mặt phẳng (SIJ): Kẻ IH ⊥ (SAB) => IH = d(I;(SAB)) = 24 (cm)
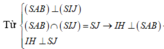
Vậy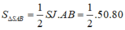
= 2000
c
m
2
1 tháng 4 2016
a) Đường sinh l của hình nón là:
l = =
= 5√41 (cm).
Diện tích xung quanh của hình nón là:
Sxq = πrl = 125π√41 (cm2)
b) Vnón = = (625.20π)/3 = (12500π)/3 (cm3)
c) Giả sử thiết diện cắt hình tròn đáy theo đoạn thẳng AB.
GỌi I là trung điểm AB, O là đỉnh của nón thì thiết diện là tam giác cân OAB.
Hạ HK vuông góc AI, H là tâm của đáy, thì HK vuông góc ( OAB) và theo giả thiết HK = 12 (cm)
