Cho tứ diện ABCD. Trên các cạnh AB,AD lấy M,N sao cho MB=2MA, NA=2ND. Mặt phẳng qua MN song song với AC chia khối tứ diện thành 2 phần. Tính tỉ số thể tích lớn hơn 1 giữa hai phần.....e cảm ơn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
16 tháng 2 2019
Chọn B.
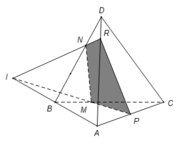
Lời khuyên cho giáo viên nên cho học sinh biết định lý Menelauyt để làm trắc nghiệm về phần này cho nhanh, việc chứng minh định lý cũng hoàn toàn đơn giản (dựa vào Talet).
Chắc chắn ta cần tính tỉ số I B I A và D R D A
Theo Menelauyt, ta có
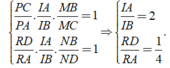
Suy ra M là trọng tâm của tam giác CAI
![]()
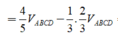
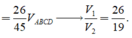
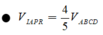
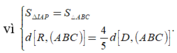
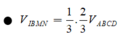
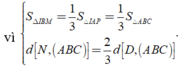
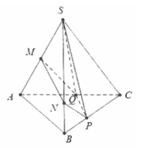
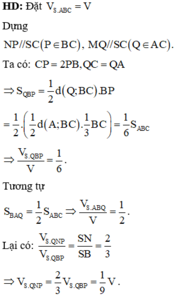


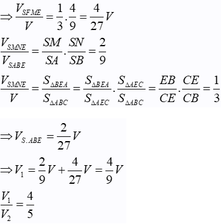
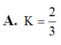
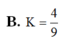
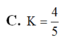
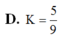
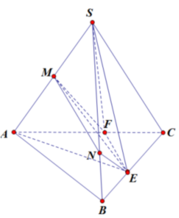


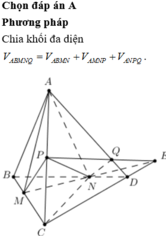

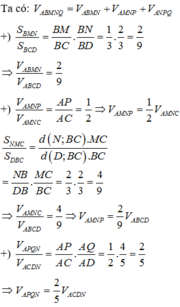

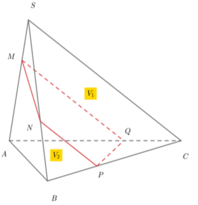

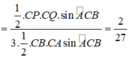
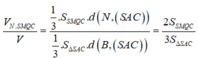
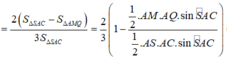
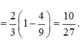
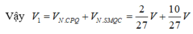
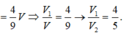
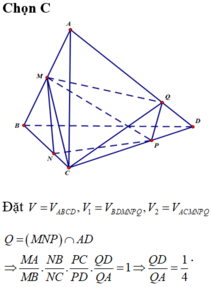
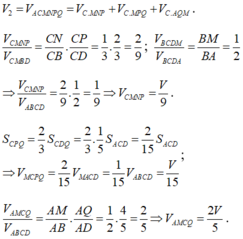
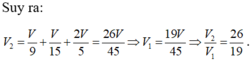
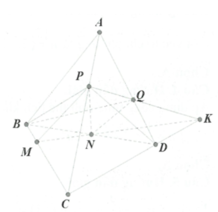


Kẻ \(MP\) và \(NQ\) lần lượt song song AC \(\Rightarrow MNQP\) là thiết diện
Kéo dài \(BD;MN;PQ\) đồng quy tại E (theo tính chất giao tuyến 3 mặt phẳng)
Áp dụng định lý Talet ta có \(DQ=\frac{1}{3}CD\) ; \(BP=\frac{2}{3}BC\)
\(\Rightarrow PB=2PC\) ; \(QC=2QD\)
Áp dụng định lý Menelaus cho tam giác \(BCD\) với 3 điểm thẳng hàng P; Q; E ta có:
\(\frac{PB}{PC}.\frac{QC}{QD}.\frac{ED}{EB}=1\) \(\Leftrightarrow\frac{2}{1}.\frac{2}{1}.\frac{ED}{EB}=1\Rightarrow ED=\frac{1}{4}EB\Rightarrow DB=3ED\)
\(\Rightarrow d\left(E;CD\right)=\frac{1}{3}d\left(B;CD\right)\)
\(\Rightarrow S_{\Delta EDQ}=\frac{1}{2}DQ.d\left(E;CD\right)=\frac{1}{2}.\frac{1}{3}CD.\frac{1}{3}d\left(B;CD\right)=\frac{1}{9}S_{\Delta BCD}\)
\(S_{BDQP}=S_{BCD}-S_{CPQ}=S_{BCD}-\frac{1}{2}.CP.d\left(Q;BC\right)\)
\(=S_{BCD}-\frac{1}{2}.\frac{1}{3}BC.\frac{2}{3}d\left(D;BC\right)=S_{BCD}-\frac{2}{9}S_{BCD}=\frac{7}{9}S_{BCD}\)
\(\Rightarrow S_{EBP}=\frac{8}{9}S_{BCD}\)
\(\Rightarrow V_{M.EBP}=\frac{1}{3}S_{EBP}.d\left(M;\left(BCD\right)\right)=\frac{1}{3}.\frac{8}{9}S_{BCD}.\frac{2}{3}d\left(A;BCD\right)=\frac{16}{27}V_{A.BCD}\)
\(V_{N.EDQ}=\frac{1}{3}S_{EDQ}.d\left(N;\left(BCD\right)\right)=\frac{1}{3}.\frac{1}{9}S_{BCD}.\frac{1}{3}d\left(A;\left(BCD\right)\right)=\frac{1}{27}V_{A.BCD}\)
\(\Rightarrow V_1=V_{BMP.DNQ}=\left(\frac{16}{27}-\frac{1}{27}\right)V_{A.BCD}=\frac{15}{27}V_{ABCD}\)
\(\Rightarrow V_2=V_{ABCD}-V_1=\frac{12}{27}V_{ABCD}\)
\(\Rightarrow\frac{V_1}{V_2}=\frac{15}{12}=\frac{5}{4}\)
// Dài quá, chắc chắn đây ko phải là cách tối ưu :(
E cảm ơn ạ