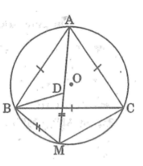
Cho tam giác ABC đều nội tiếp đường tròn (O). Trên cung nhỏ AB lấy điểm M, trên dây MC lấy điểm N sao cho MB = CN.a) Chứng minh rằng tam giác AMN đều.b) Kẻ đường kính BD của đường tròn (O). Chứng minh MD là đường trung trực của đoạnthẳng AN.c) Tiếp tuyến kẻ từ D với đường tròn (O) cắt tia BA và tia MC lần lượt tại T, K. Tính số đobằng độ của tổng hai góc: ··NAT NKT+.d) Khi M di động...
Đọc tiếp
Cho tam giác ABC đều nội tiếp đường tròn (O). Trên cung nhỏ AB lấy điểm M, trên dây MC lấy điểm N sao cho MB = CN.a) Chứng minh rằng tam giác AMN đều.b) Kẻ đường kính BD của đường tròn (O). Chứng minh MD là đường trung trực của đoạnthẳng AN.c) Tiếp tuyến kẻ từ D với đường tròn (O) cắt tia BA và tia MC lần lượt tại T, K. Tính số đobằng độ của tổng hai góc: ··NAT NKT+.d) Khi M di động trên cung nhỏ AB, hãy xác định vị trí của điểm M để tổng của hai đoạnthẳng MA + MB lớn nhất
a ) Ta có BM=MD (gt)
=> ΔΔMBD cân tại M
Mặt khác AMBˆ=ACBˆAMB^=ACB^ ( Hai góc nội tiếp chắn cung AB)
Mà ACBˆ=600ACB^=600( tam giác ABC đều)
Suy ra AMBˆ=600hayDMBˆ=600AMB^=600hayDMB^=600
Vậy ΔMBDΔMBD đều
b) Ta có ΔMBDΔMBD đều ( CMT)
Suy ra : DMBˆ=DBCˆ+CBMˆ=600DMB^=DBC^+CBM^=600(1)
Lại có : tam giác ABC đều (gt)
Suy ra : ABCˆ=ABDˆ+DBCˆ=600ABC^=ABD^+DBC^=600(2)
Từ (1) và (2) suy ra ABDˆ=MBCˆABD^=MBC^
Xét hai tam giác ABD và CBM ta có
BC=BA (gt)
ABDˆ=MBCˆ(cmt)ABD^=MBC^(cmt)
BD=BM( tam giác MBD đều)
=> ΔABD=ΔCBM(c.g.c)ΔABD=ΔCBM(c.g.c)
c)ΔABD=ΔCBM(cmt)ΔABD=ΔCBM(cmt)
SUy ra AD=CM
mà AM=AD+DM
SUy ra MA=MC+MD