Cho phương trình bậc hai ax2+bx+c=0 có 2 nghiệm là x1 và x2. Lập phương trình bậc hai có 2 nghiệm là 2x1+3x2 và 3x1 + 2x2 .
Giải giúp mình với ạ . Chi tiết chút ^^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 6 2023
x1+x2=-b/a; x1x2=c/a
=>2x1+2x2=-2b/a; 4x1x2=4c/a
=>PT cần tìm là x^2+2b/a*x+4c/a=0
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 9 2021
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-2\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}y_1+y_2=2x_1-x_2+2x_2-x_1\\y_1y_2=\left(2x_1-x_2\right)\left(2x_2-x_1\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=x_1+x_2\\y_1y_2=-2x_1^2-2x_2^2+5x_1x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=-\dfrac{5}{3}\\y_1y_2=-2\left(x_1+x_2\right)^2+9x_1x_2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=-\dfrac{5}{3}\\y_1y_2=-2.\left(-\dfrac{5}{3}\right)^2+9.\left(-2\right)=-\dfrac{212}{9}\end{matrix}\right.\)
\(\Rightarrow y_1;y_2\) là nghiệm của:
\(y^2+\dfrac{5}{3}y-\dfrac{212}{9}=0\Leftrightarrow9y^2+10y-212=0\)
30 tháng 5 2021
\(x^2-2x-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}u=x_1+\left(x_2\right)^2\\v=x_2+\left(x_1\right)^2\end{matrix}\right.\)
\(\Rightarrow\)\(\left\{{}\begin{matrix}u+v=\left(x_1+x_2\right)+\left(x_2+x_1\right)^2-2x_1x_2\\uv=2x_1x_2+x_1^3+x_2^3=2x_1x_2+\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u+v=8\\uv=12\end{matrix}\right.\)
=>u và v là nghiệm của pt \(t^2-8t+12=0\)
CM
11 tháng 4 2019
1) Với m= 2 PT trở thành x 2 − 4 x + 3 = 0
Giải phương trình tìm được các nghiệm x = 1 ; x = 3.
2) Ta có Δ ' = m 2 − m 2 + 1 = 1 > 0 , ∀ m .
Do đó, phương trình (1) luôn có hai nghiệm phân biệt.
Từ giả thiết ta có x i 2 − 2 m x i + m 2 − 1 = 0 , i = 1 ; 2. x i 3 − 2 m x i 2 + m 2 x i − 2 = x i x i 2 − 2 m x i + m 2 − 1 + x i − 2 = x i − 2 , i = 1 ; 2.
Áp dụng định lí Viét cho phương trình (1) ta có x 1 + x 2 = 2 m ; x 1 . x 2 = m 2 − 1
Ta có
x 1 − 2 + x 2 − 2 = 2 m − 4 ; x 1 − 2 x 2 − 2 = x 1 x 2 − 2 x 1 + x 2 + 4 = m 2 − 1 − 4 m + 4 = m 2 − 4 m + 3
Vậy phương trình bậc hai nhận x 1 3 − 2 m x 1 2 + m 2 x 1 − 2 , x 2 3 − 2 m x 2 2 + m 2 x 2 − 2 là nghiệm là x 2 − 2 m − 4 x + m 2 − 4 m + 3 = 0.
CM
24 tháng 3 2017
Đáp án: D
Theo định lý Vi-ét ta có
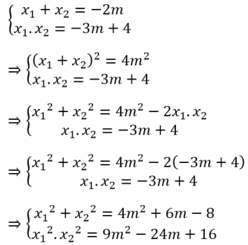
Khi đó, 
là nghiệm của phương trình
CM
30 tháng 8 2017
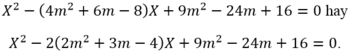
* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
Bài làm
\(ax^2+bx+c=0\)
Theo định lý Viet :
\(\hept{\begin{cases}x_1+x_2=\frac{-b}{a}\\x_1\cdot x_2=\frac{c}{a}\end{cases}}\)
Ta có:\(\hept{\begin{cases}\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=5\left(x_1+x_2\right)\\\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=6x_1^2+4x,x_2+6x^2_2+9x,x_2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=\frac{-5b}{a}\\\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=6\left(x_1+x_2\right)^2+x_1\cdot x_2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=\frac{-5b}{a}\\\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=\frac{+6b^2}{a^2}+\frac{c}{a}\end{cases}}\)
Vậy \(\left(2x_1+3x_2\right)\)và \(\left(3x_1+2x_2\right)\)là n của pt:
\(X^2-\left(\frac{-5b}{a}\right)X+\frac{6b^2}{a^2}+\frac{c}{a}=0\)
\(X^2+\frac{5b}{a}X+\frac{6b^2}{a^2}+\frac{c}{a}=0\)
~Hok tốt nhé~