Tìm tất cả các giá trị tham số m dể phương trình
\(\frac{1}{3}\)\(\left|cos^3x\right|\)-3cos2x+5\(\left|Cosx\right|\)-3+2m=0
có đúng 4 nghiệm phân biệt thuộc đoạn\(\left[0;2\pi\right]\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 2 2018
Chọn C.
Phương pháp:
Giải phương trình bằng phương pháp đặt ẩn phụ.
Cách giải:
HP
1 tháng 8 2021
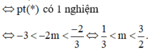
1.
\(cos2x-3cosx+2=0\)
\(\Leftrightarrow2cos^2x-3cosx+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(x=k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow\) không có nghiệm x thuộc đoạn
\(x=\pm\dfrac{\pi}{3}+k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow x_1=\dfrac{\pi}{3};x_2=\dfrac{5\pi}{3}\)
\(\Rightarrow P=x_1.x_2=\dfrac{5\pi^2}{9}\)
HP
1 tháng 8 2021
2.
\(pt\Leftrightarrow\left(cos3x-m+2\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\left(1\right)\\cos3x=m-2\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\)
Ta có: \(x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\pm\dfrac{\pi}{9}\)
Yêu cầu bài toán thỏa mãn khi \(\left(2\right)\) có nghiệm duy nhất thuộc \(\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=0\\m-2=1\\m-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=3\\m=1\end{matrix}\right.\)
TH1: \(m=2\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\dfrac{\pi}{6}\left(tm\right)\)
\(\Rightarrow m=2\) thỏa mãn yêu cầu bài toán
TH2: \(m=3\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=0\left(tm\right)\)
\(\Rightarrow m=3\) thỏa mãn yêu cầu bài toán
TH3: \(m=1\)
\(\left(2\right)\Leftrightarrow cos3x=-1\Leftrightarrow x=\dfrac{\pi}{3}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{1}{3}\\x=-1\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow m=2\) không thỏa mãn yêu cầu bài toán
Vậy \(m=2;m=3\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
\(\Delta'=\left(m+1\right)^2-\left(m^2+2m\right)=1>0\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=m+1-1=m\\x_2=m+1+1=m+2\end{matrix}\right.\)
\(\left|x_1\right|=3\left|x_2\right|\Leftrightarrow\left|m\right|=3\left|m+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3m+6=-m\\3m+6=m\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{3}{2}\\m=-3\end{matrix}\right.\)
14 tháng 6 2023
Δ=(2m-1)^2-4(2m-2)
=4m^2-4m+1-8m+8=(2m-3)^2
Để pt có 2 nghiệm pb thì 2m-3<>0
=>m<>3/2
x1^4+x2^4=17
=>(x1^2+x2^2)^2-2(x1x2)^2=17
=>[(2m-1)^2-2(2m-2)]^2-2(2m-2)^2=17
=>[4m^2-4m+1-4m+4]^2-2(4m^2-8m+4)=17
=>(4m^2-8m+5)^2-2(4m^2-8m+4)=17
Đặt 4m^2-8m+4=a
Ta sẽ có (a+1)^2-2a-17=0
=>a^2-16=0
=>a=4 hoặc a=-4(loại)
=>4m^2-8m=0
=>m=0 hoặc m=2
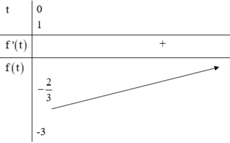
Đặt \(\left|cosx\right|=a\Rightarrow0\le a\le1\)
Phương trình trở thành \(\frac{1}{3}a^3-3a^2+5a-3+2m=0\) (1)
Để phương trình ban đầu có đúng 4 nghiệm pb thuộc \(\left[0;2\pi\right]\) \(\Leftrightarrow\left(1\right)\) có nghiệm duy nhất thuộc \(\left(0;1\right)\)
Xét \(f\left(a\right)=\frac{1}{3}a^3-3a^2+5a-3\)
\(f'\left(a\right)=a^2-6a+5=0\Rightarrow\left[{}\begin{matrix}a=1\\a=5\end{matrix}\right.\) \(\Rightarrow f\left(a\right)\) đồng biến trên \(\left(0;1\right)\)
\(f\left(0\right)=-3\); \(f\left(1\right)=-\frac{2}{3}\)
\(\Rightarrow-3< -2m< -\frac{2}{3}\Rightarrow\frac{1}{3}< m< \frac{3}{2}\)