Một xe chuyển động trên đường thẳng AB theo một chiều, trong 1/3 thời gian đầu xe chạy với vận tốc 50km/h, trong 2/3 thời gian sau xe chạy với vận tốc 40km/h. Tính vận tốc trung bình của xe trên đoạn đường AB?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
9 tháng 11 2023
Vận tốc TB của xe suốt thời gian chạy trên trường:
\(v_{tb}=\dfrac{v_1t_1+v_2t_2}{t_1+t_2}=\dfrac{60.2+40.3}{2+3}=48\left(\dfrac{km}{h}\right)\)
VT
9 tháng 12 2017
Đáp án B
- Mà quãng đường ô tô đi trong 2 giờ đầu là:
2.50 = 100 (km)
- Quãng đường ô tô đi trong 3 giờ sau là:
3.40 = 120 (km)
- Vận tốc trung bình của xe trong suốt thời gian chuyển động là:
(100 + 120) : (2 + 3) = 44 (km/h)
TK
25 tháng 9 2021
Vận tốc trung bình của xe trên đoạn đường AB
\(v=\dfrac{s}{t}=\dfrac{s_1+s_2}{t}=\dfrac{\dfrac{v_1}{2}t+\dfrac{v_2}{2}t}{t}=\dfrac{t\dfrac{\left(v_1+v_2\right)}{2}}{t}=\dfrac{v_1+v_2}{2}=\dfrac{40+50}{2}=45\left(\dfrac{km}{h}\right)\)
TK
28 tháng 8 2021
Vận tốc trung bình của xe trên quãng đường còn lại là
\(v'=\dfrac{t\left(\dfrac{2v_2}{3}+\dfrac{v_3}{3}\right)}{t}=\dfrac{1\left(\dfrac{2\cdot50}{3}+\dfrac{40}{3}\right)}{1}=\dfrac{140}{3}\left(\dfrac{km}{h}\right)\)
Vận tốc trung bình trên cả quảng đường là
\(v=\dfrac{s}{s\left(\dfrac{1}{3v_1}+\dfrac{2}{3v'}\right)}=\dfrac{1}{1\left(\dfrac{1}{3\cdot60}+\dfrac{2}{3\cdot\dfrac{140}{3}}\right)}=50,4\left(\dfrac{km}{h}\right)\)
TK
28 tháng 8 2021
Bạn nếu có phát hiện chỗ sai hay ko hiểu về cách giải của mình thì có thể ib hỏi nha. Mình giải có hơi tắt ý. Chúc bạn một ngày tốt lành!
VT
15 tháng 9 2017
Chọn đáp án D
Tổng quãng đường xe chạy là Δ s = 50.2 + 35.3 = 205 km.
G
20 tháng 12 2021
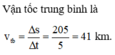
2 giờ đầu xe chạy đc quãng đường:
\(s_1=60.2=120\left(km\right)\)
3h sau xe chạy đc quãng đường:
\(s_2=40.3=120\left(km\right)\)
vận tốc trung bình của xe trong suốt thời gian chạy:
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{120+120}{2+3}=48\) (km/h)