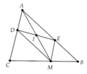
Cho tam giác ABC cân tại A, một điểm F di động trên cạnh AC và F không trùng với điểm A.
1) Xác định điểm E nằm trên đường thẳng AB sao cho trung điểm I của đoạn thẳng EF nằm trên cạnh BC.
2) Chứng minh rằng với điểm E xác định ở trên thì tâm đường tròn ngoại tiếp tam giác AEF nằm trên một đường thẳng cố định