Phương trình cos3x = cos x có bao nhiêu nghiệm thuộc khoảng (0; 2017π) ?
A. 2016 B. 5049 C. 3033 D. 5051
Cho em hỏi luôn ạ ,em giải ra 6049 mà ko có đáp án vậy em sai hay đề sai vậy ạ? TvT
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow3sinx-4sin^3x+4cos^3x-3cosx+2cosx=0\)
\(\Leftrightarrow3sinx-cosx-4sin^3x+4cos^3x=0\)
Với \(cosx=0\) ko phải nghiệm, với \(cosx\ne0\) chia 2 vế cho \(cos^3x\)
\(\Leftrightarrow3tanx\left(1+tan^2x\right)-\left(1+tan^2x\right)-4tan^3x+4=0\)
\(\Leftrightarrow-tan^3x-tan^2x+3tanx+3=0\)
\(\Leftrightarrow-tan^2x\left(tanx+1\right)+3\left(tanx+1\right)=0\)
\(\Leftrightarrow\left(tanx+1\right)\left(3-tan^2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\sqrt{3}\\tanx=-\sqrt{3}\end{matrix}\right.\)
Tới đây chắc bạn hoàn thành được phần còn lại

Đáp án A
Dùng công thức ![]() để đưa phương trình ban đầu về đa thức bậc 2 theo sin x.
để đưa phương trình ban đầu về đa thức bậc 2 theo sin x.
Giải phương trình này tìm x và đối chiếu với yêu cầu ![]() để tìm được giá trị của x.
để tìm được giá trị của x.
Ta có
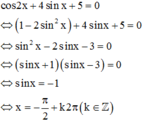
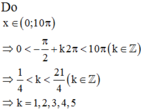
Do đó tập nghiệm của phương trình đã cho trên 0 ; 10 π là
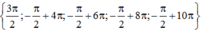
\(\Leftrightarrow\left[{}\begin{matrix}3x=x+k2\pi\\3x=-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\)
\(0< \dfrac{k\pi}{2}< 2017\pi\Rightarrow0< k< 4034\)
Có \(4033\) nghiệm (tất cả các đáp án đều sai)