Bài 1 : Cho Δ ABC có 3 góc nhọn , AB = 2cm , AC = 4cm . Trên cạnh AC lấy điểm M sao cho \(\widehat{ABM}=\widehat{ACB}\) .
a, Chứng minh : Δ ABM ∼ ΔACB
b, Tính AM
c, Từ A kẻ AH ⊥ BC , AK ⊥ BM . Chứng minh AB.AK=AM.AH
d , chứng ming rằng : SAHB = 4SAKM
Bài 2 : Cho Δ ABC vuông tại A , có \(\widehat{B}=\widehat{2C}\) , đường cao AD .
a, Chứng minh : ΔADB ∼ ΔCAB
b, Kẻ tia phân giác \(\widehat{ABC}\) cắt AD tại F và AC tại E . Chứng minh AB2 =...
Đọc tiếp
Bài 1 : Cho Δ ABC có 3 góc nhọn , AB = 2cm , AC = 4cm . Trên cạnh AC lấy điểm M sao cho \(\widehat{ABM}=\widehat{ACB}\) .
a, Chứng minh : Δ ABM ∼ ΔACB
b, Tính AM
c, Từ A kẻ AH ⊥ BC , AK ⊥ BM . Chứng minh AB.AK=AM.AH
d , chứng ming rằng : SAHB = 4SAKM
Bài 2 : Cho Δ ABC vuông tại A , có \(\widehat{B}=\widehat{2C}\) , đường cao AD .
a, Chứng minh : ΔADB ∼ ΔCAB
b, Kẻ tia phân giác \(\widehat{ABC}\) cắt AD tại F và AC tại E . Chứng minh AB2 = AE.AC
c, Chứng minh : \(\frac{DF}{FA}=\frac{AE}{EC}\)
d, Tính tỷ số diện tích của ΔBFC và ΔABC .
Bài 3 : Cho tam giác ABC vuông tại A , đường cao AH chia cạnh huyền BC thành hai đoạn BH = 9cm và CH =16cm .
a, Chứng minh : ΔABH ∼ ΔCAH ; Tính diện tích ΔABC
b, Gọi M , N lần lượt là trung điểm của AH và HC . Đường thẳng BM cắt AN tại K . Chứng minh : MK là đường cao của ΔAMN .
c, Gọi D là điểm đối xứng của C qua điểm A . Chứng minh : AB.DH= 2AD.BM
các bạn ơi ! giúp mình với đi !!!!!!!!!!!!!!!!!!!!

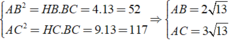
a) - Xét △ABH và △CAH có :
∠AHB = ∠CHA ( =90o )
∠BAH = ∠ACH ( cùng phụ với ∠ABC )
=> △ABH ∼ △CAH (g-g)
- Áp dụng hệ thức lượng vào △ABC vuông tại A đường cao AH có :
AH2 = BH . CH = 16 . 9 = 144 => AH = 12(cm)
Diện tích △ABC = \(\frac{1}{2}\)AH.BC = \(\frac{1}{2}\).12.25 = 150 ( cm2 )