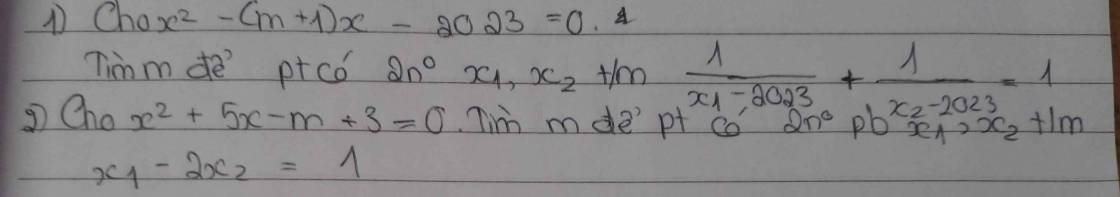Giúp tớ với ạ cảm ơn trc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mặt phẳng thì không có bờ, chỉ có nửa mặt phẳng mới có bờ là một đường thẳng nào đó thôi.
Mặt phẳng tới và mặt phẳng khúc xạ là một. Nó chính là cái mặt phẳng trang giấy bạn vẽ hình đấy. Người ta phân biết bằng tên chỉ đến nhấn mạnh rằng: Mặt phẳng tới thì chú ý phần phía trên ấy, chỗ tia sáng đi tới, còn mặt phẳng khúc xạ thì chú ý phần bên dưới, chỗ có tia bị gẫy khúc.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{b-a}{4-3}=23\)
Do đó: a=69; b=92

\(A=\dfrac{1}{2}+\dfrac{2}{4}+\dfrac{3}{8}+...+\dfrac{10}{2^{10}}\)
\(2A=\dfrac{1}{1}+\dfrac{2}{2}+\dfrac{3}{4}+...+\dfrac{10}{2^9}\)
\(2A-A=\left(1+\dfrac{2}{2}+\dfrac{3}{4}+...+\dfrac{10}{2^9}\right)-\left(\dfrac{1}{2}+\dfrac{2}{4}+...+\dfrac{10}{2^{10}}\right)\)
\(A=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^9}-\dfrac{10}{2^{10}}\)
\(B=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^9}\)
\(2B=2+1+\dfrac{1}{2}+...+\dfrac{1}{2^8}\)
\(2B-B=\left(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^8}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^9}\right)\)
\(B=2-\dfrac{1}{2^9}\)
Suy ra \(A=B-\dfrac{10}{2^{10}}=2-\dfrac{1}{2^9}-\dfrac{10}{2^{10}}=\dfrac{509}{256}\)


1: \(x^2-\left(m+1\right)x-2023=0\)
a=1; b=-(m+1); c=-2023
Vì \(a\cdot c=-2023< 0\)
nên phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left[-\left(m+1\right)\right]}{1}=m+1\\x_2\cdot x_1=\dfrac{c}{a}=-\dfrac{2023}{1}=-2023\end{matrix}\right.\)
\(\dfrac{1}{x_1-2023}+\dfrac{1}{x_2-2023}=1\)
=>\(\dfrac{x_2-2023+x_1-2023}{\left(x_1-2023\right)\left(x_2-2023\right)}=1\)
=>\(x_2+x_1-4046=\left(x_1-2023\right)\left(x_2-2023\right)\)
=>\(m+1-4046=x_1x_2-2023\left(x_1+x_2\right)+2023^2\)
=>\(m-4045=-2023-2023\left(m+1\right)+2023^2\)
=>\(m-4045=-2023-2023m-2023+2023^2\)
=>\(2024m=4092528\)
=>\(m=\dfrac{4092528}{2024}=2022\)

\(b,\sqrt{36}.\sqrt{\dfrac{25}{26}}+\dfrac{1}{4}\\ =\sqrt{6^2}.\sqrt{\left(\dfrac{5}{4}\right)^2}+\dfrac{1}{4}\\=6.\dfrac{5}{4}+\dfrac{1}{4}=\dfrac{30}{4}+\dfrac{1}{4}=\dfrac{31}{4}\)
\(c,\sqrt{\dfrac{4}{81}}:\sqrt{\dfrac{25}{81}}-1\dfrac{2}{5}\\ =\sqrt{\left(\dfrac{2}{9}\right)^2}:\sqrt{\left(\dfrac{5}{9}\right)^2}-\dfrac{7}{5}\\ =\dfrac{2}{9}:\dfrac{5}{9}-\dfrac{7}{5}\\ =\dfrac{2}{9}.\dfrac{9}{5}-\dfrac{7}{5}=\dfrac{2}{5}-\dfrac{7}{5}\\ =-1\)
\(d, 0,1.\sqrt{225}.\sqrt{\dfrac{1}{4}}\\ =\dfrac{1}{10}.\sqrt{15^2}.\sqrt{\left(\dfrac{1}{2}\right)^2}\\ =\dfrac{1}{10}.15.\dfrac{1}{2}=\dfrac{3}{5}\)
\(e, \dfrac{3^{25}}{9^3.3^{16}}\\ =\dfrac{3^{25}}{\left(3^2\right)^3.3^{16}}\\ =\dfrac{3^{25}}{3^6.3^{16}}\\ =\dfrac{3^{25}}{3^{22}}\\ =3^3=27\)