Cho x, y nguyên thỏa mãn x2 + 4x + y2 - 12 = 0. Khi đó giá trị lớn nhất P = x2 + y2 là Pmax =?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
11 tháng 11 2015
4x^2 + 4x + y^2 - 12=0
<=> 4x^2 +4x +1 +y^2 -13=0
<=> (2x +1)^2 x + y^2=13 (1)
Vì x; y là số nguyên => (2x +1)^2 ; y^2 là 1 số chính phương
Mà 13=2^2 +3^2
Từ (1) => (2x + 1)^2=2 ^2 ; y^2=3^2 hoặc (2x +1)^2=3^2 ; y^2=2^2
.............
(Tự làm nốt bằng cách tìm ra x; y cụ thể rồi thay vào)
CM
22 tháng 2 2019
Chọn B.
Phương pháp:
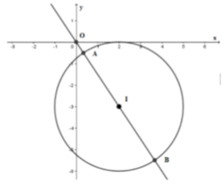
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
CM
19 tháng 9 2018
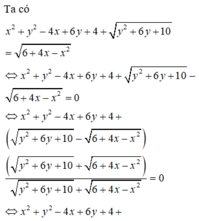
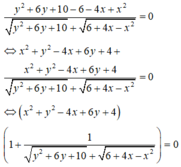
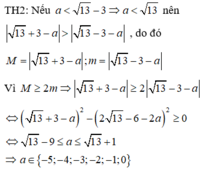
Đáp án C.
Phương pháp giải: Dựa vào giả thiết, đánh giá đưa về tổng các bình phương, từ biểu thức P đưa về hạng tử trong tổng bình phương và áp dụng bất đẳng thức Bunhiacopxki tìm giá trị lớn nhất.
Lời giải:
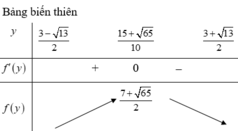
Vì x2 + y2 > 1 suy ra log x 2 + y 2 f ( x ) là hàm số đồng biến trên tập xác định
Khi đó 
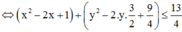
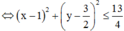
Xét biểu thức P, ta có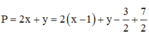 
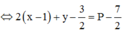
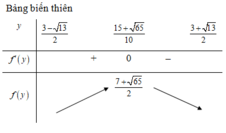
Áp dụng BĐT Bunhiacopxki, có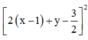 
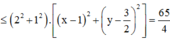
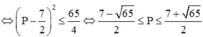
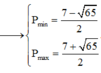
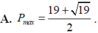
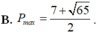
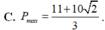
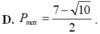
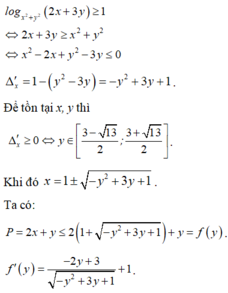
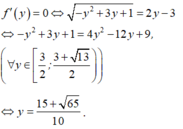
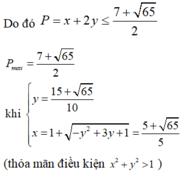
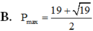
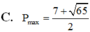
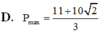
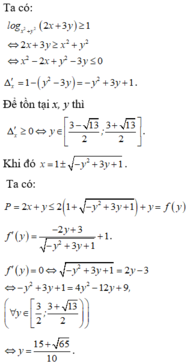
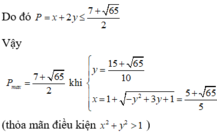
x2 +4x+y2-12 =0 => (x+2)2 =(4-y)(4+y) ; vì x;y thuộc Z => 4-y = 4+y => y =0 => (x+2)2 =16
x +2 = 4 => x =2
hoăc x+2 =-4 => x =-6
=> Pmax=x2 +y2 = (-6)2 +0 = 36 khi x = -6; y =0