tìm các giá trị của x thỏa mãn \(x^2< 2x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VA
1
4 tháng 5 2019
giúp. Mk đang cần gấp<=> x2 + 2x2y2 + 2y2 - x2y2 + 2x2 - 2 = 0
<=> -x2 + x2y2 + 2y2 - 2 = 0
<=> x2 (y2 - 1) + 2 (y2 - 1) = 0
<=> (x2 + 2)(y2 - 1) = 0
Vì x2 ≥0 với mọi x => y2 - 1 = 0 <=> y = -1 và y = 1.
Vậy x ∈R , y = {-1;1}
NC
2
VV
3 tháng 11 2017
vì (2x-3).(x-1/4) <0
=> 2x-3 và x-1/4 khác dấu
=> \(\orbr{\begin{cases}\hept{\begin{cases}2x-3< 0\\x-\frac{1}{4}>0\end{cases}}\\\hept{\begin{cases}2x-3>0\\x-\frac{1}{4}< 0\end{cases}}\end{cases}}\)
+ Nếu \(\hept{\begin{cases}2x-3< 0\\x-\frac{1}{4}>0\end{cases}}\) => \(\hept{\begin{cases}2x< 3\\x>\frac{1}{4}\end{cases}}\) => \(\hept{\begin{cases}x< \frac{3}{2}\\x>\frac{1}{4}\end{cases}}\) => \(\frac{1}{4}< x< \frac{3}{2}\)
+Nếu \(\hept{\begin{cases}2x-3>0\\x-\frac{1}{4}< 0\end{cases}}\)=> \(\hept{\begin{cases}2x>3\\x< \frac{1}{4}\end{cases}}\) => \(\hept{\begin{cases}x>\frac{3}{2}\\x< \frac{1}{4}\end{cases}}\)(vô lý) => loại
Vậy \(\frac{1}{4}< x< \frac{3}{2}\)
17 tháng 7 2016
vì x > 2 mà lại nhỏ hơn hoặc =4 nên x có 2 nghiệm là 3; 4 thỏa mãn
cũng như bn có số quả táo nhiều hơn 2 mà ít hơn 5 thì bn có 3 hoặc 4 quả
17 tháng 7 2016
3-2x <= 15-5x
5x-2x <= 15-3
x<= 4
3-2x <7
x>2
kết hợp nghiệm ta có;
2<x<=4
vậy x = 3; 4 thỏa mãn
11 tháng 9 2016
\(2\cdot2^2\cdot2^3\cdot2^4\cdot\cdot\cdot2^x=32768\)
\(\Leftrightarrow2^{1+2+3+4+\cdot\cdot\cdot+x}=2^{15}\)
\(\Leftrightarrow1+2+3+4+..+x=15\)
\(\Leftrightarrow\)\(\frac{\left(1+x\right)x}{2}=15\)
\(\Leftrightarrow x\left(x+1\right)=30=5\left(5+1\right)\)
Vậy x=5
Bài 2:
Bậc của đơn thức là 2+5+3=10
Bài 3:
\(\left|2x-\frac{1}{2}\right|+\frac{3}{7}=\frac{38}{7}\)
\(\Leftrightarrow\left|2x-\frac{1}{2}\right|=5\)
+)TH1: \(x\ge\frac{1}{4}\) thì bt trở thành
\(2x-\frac{1}{2}=5\Leftrightarrow2x=\frac{11}{2}\Leftrightarrow x=\frac{11}{4}\left(tm\right)\)
+)TH2: \(x< \frac{1}{4}\) thì pt trở thành
\(2x-\frac{1}{2}=-5\Leftrightarrow2x=-\frac{9}{2}\Leftrightarrow x=-\frac{9}{4}\left(tm\right)\)
Vậy x={-9/4;11/4}
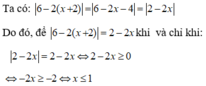
\(x^2< 2x\)
\(\Leftrightarrow x^2-2x< 0\)
\(\Leftrightarrow x\left(x-2\right)< 0\)
TH1:\(\hept{\begin{cases}x< 0\\x-2>0\end{cases}\left(l\right)}\)
TH2:\(\hept{\begin{cases}x>0\\x-2< 0\end{cases}\Leftrightarrow0< x< 2\left(n\right)}\)
V...