Giải phương trình
(3x2 - 6x)(\(\sqrt{2x-1}+1\)) = 2x3 - 5 x2 +4x - 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 7 2019
3x2 + 2x - 1 = 0
=> 3x2 + 3x - x - 1 = 0
=> 3x(x + 1) - (x + 1) = 0
=> (3x - 1)(x + 1) = 0
=> \(\orbr{\begin{cases}3x-1=0\\x+1=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=\frac{1}{3}\\x=-1\end{cases}}\)
x2 - 5x + 6 = 0
=> x2 - 2x - 3x + 6 = 0
=> x(x - 2) - 3(x - 2) = 0
=> (x - 3)(x - 2) = 0
=> \(\orbr{\begin{cases}x-3=0\\x-2=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=3\\x=2\end{cases}}\)
3x2 + 7x + 2 = 0
=> 3x2 + 6x + x + 2 = 0
=> 3x(x + 2) + (x + 2) = 0
=> (3x + 1)(x + 2) = 0
=> \(\orbr{\begin{cases}3x+1=0\\x+2=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=-\frac{1}{3}\\x=-2\end{cases}}\)
5 tháng 7 2019
1, \(3x^2+2x-1=0\Leftrightarrow3x^2+3x-x-1=0\)
\(\Leftrightarrow3x\left(x+1\right)-\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\3x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{1}{3}\end{cases}}}\)
2, \(x^2-5x+6=0\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}}\)
3, \(3x^2+7x+2=0\Leftrightarrow3x^2+6x+x+2=0\)
\(\Leftrightarrow3x\left(x+2\right)+\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\3x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-\frac{1}{3}\end{cases}}}\)
CM
11 tháng 2 2019
Đặt và thực hiện phép tính ta có :
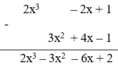
Vậy chọn đa thức thứ hai.
CM
13 tháng 3 2019
a) (x – 1)(x2 + x + 1) – 2x = x(x – 1)(x + 1)
⇔ x3 – 1 – 2x = x(x2 – 1)
⇔ x2 – 1 – 2x = x3 – x
⇔ -2x + x = 1 ⇔ - x = 1 ⇔ x = -1
Tập nghiệm của phương trình: S = { -1}
b) x2 – 3x – 4 = 0
⇔ x2 – 4x + x – 4 = 0 ⇔ x(x – 4) + (x – 4) = 0
⇔ (x – 4)(x + 1) = 0 ⇔ x – 4 = 0 hoặc x + 1 = 0
⇔ x = 4 hoặc x = -1
Tập nghiệm của phương trình: S = {4; -1}
c) ĐKXĐ : x – 1 ≠ 0 và x2 + x + 1 ≠ 0 (khi đó : x3 – 1 = (x – 1)(x2 + x + 1) ≠ 0)
⇔ x ≠ 1
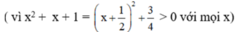
Quy đồng mẫu thức hai vế:
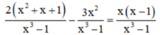
Khử mẫu, ta được: 2x2 + 2x + 2 – 3x2 = x2 – x
⇔ -2x2 + 3x + 2 = 0 ⇔ 2x2 – 3x – 2 = 0
⇔ 2x2 – 4x + x – 2 = 0 ⇔ 2x(x – 2) + (x – 2) = 0
⇔ (x – 2)(2x + 1) = 0 ⇔ x – 2 = 0 hoặc 2x + 1 = 0
⇔ x = 2 hoặc x = -1/2(thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {2 ; -1/2}
d) ĐKXĐ : x – 5 ≠ 0 và x – 1 ≠ 0 (khi đó : x2 – 6x + 5 = (x – 5)(x – 1) ≠ 0)
Quy đồng mẫu thức hai vế :
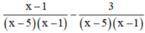
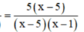
Khử mẫu, ta được : x – 1 – 3 = 5x – 25 ⇔ -4x = -21
⇔ x = 21/4 (thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {21/4}
DN
1
19 tháng 1 2022
a, \(\left(x-3\right)\left(x^2+x-20\right)\ge0\)
\(\Leftrightarrow\) \(\left(x-3\right)\left(x-4\right)\left(x+5\right)\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x+5=0\Leftrightarrow x=-5\)
+) Lập trục xét dấu f(x) (Bạn tự kẻ trục nha)
\(\Rightarrow\) Bpt có tập nghiệm S = \(\left[-5;3\right]\cup\) [4; \(+\infty\))
b, \(\dfrac{x^2-4x-5}{2x+4}\ge0\)
\(\Leftrightarrow\) \(\dfrac{\left(x-5\right)\left(x+1\right)}{2x+4}\ge0\)
+) \(x-5=0\Leftrightarrow x=5\); \(x+1=0\Leftrightarrow x=-1\); \(2x+4=0\Leftrightarrow x=-2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (-2; -1] \(\cup\) [5; \(+\infty\))
c, \(\dfrac{-1}{x^2-6x+8}\le1\)
\(\Leftrightarrow\) \(\dfrac{\left(x-3\right)^2}{\left(x-4\right)\left(x-2\right)}\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x-2=0\Leftrightarrow x=2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (\(-\infty\); 2) \(\cup\) (4; \(+\infty\))
Chúc bn học tốt!
AH
Akai Haruma
Giáo viên
22 tháng 6 2021
Lời giải:
a. ĐKXĐ: $x\geq 4$
PT $\Leftrightarrow \sqrt{(x-4)+4\sqrt{x-4}+4}=2$
$\Leftrightarrow \sqrt{(\sqrt{x-4}+2)^2}=2$
$\Leftrightarrow |\sqrt{x-4}+2|=2$
$\Leftrightarrow \sqrt{x-4}+2=2$
$\Leftrightarrow \sqrt{x-4}=0$
$\Leftrightarrow x=4$ (tm)
b. ĐKXĐ: $x\in\mathbb{R}$
PT $\Leftrightarrow \sqrt{(2x-1)^2}=\sqrt{(x-3)^2}$
$\Leftrightarrow |2x-1|=|x-3|$
\(\Rightarrow \left[\begin{matrix} 2x-1=x-3\\ 2x-1=3-x\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-2\\ x=\frac{4}{3}\end{matrix}\right.\)
c.
PT \(\Rightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 2x^2-2x+1=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ 2x^2-2x=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ 2x(x-1)=0\end{matrix}\right.\Rightarrow x=1\)