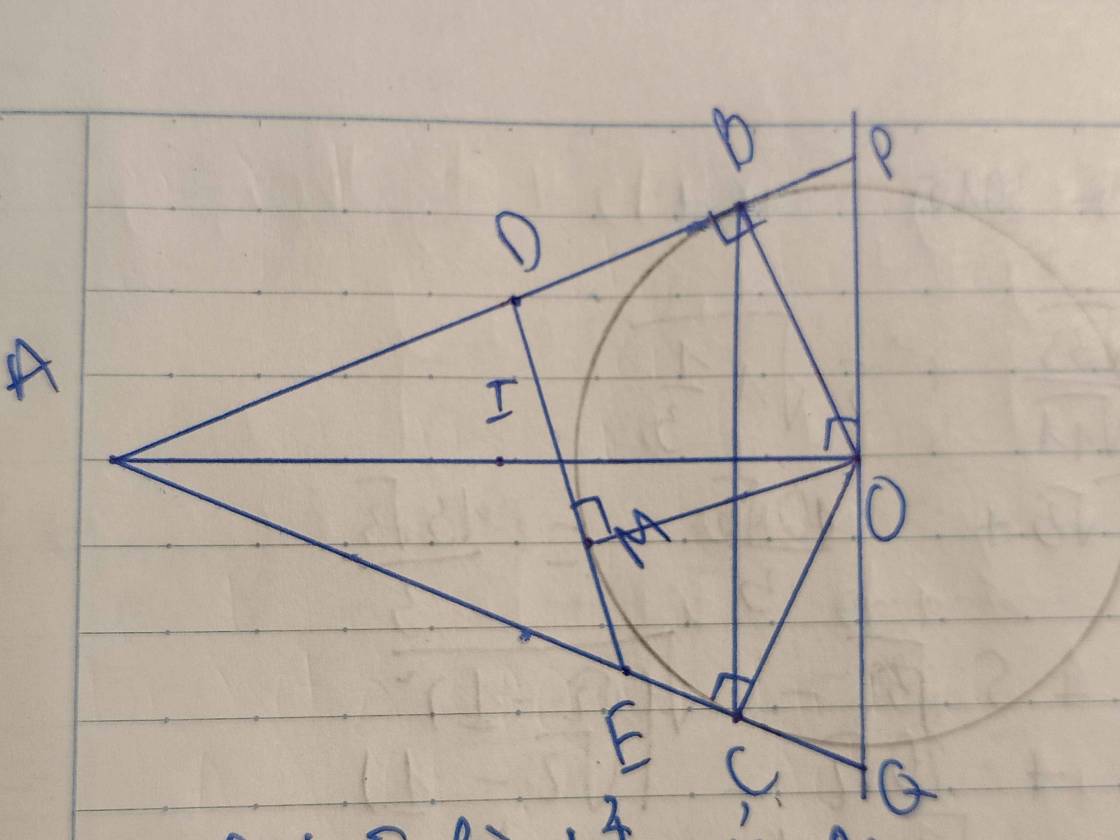
cho đường tròn (O) và một điểm A cố định nằm ngoài (O) .Kẻ tiếp tuyến AB,AC với (O) ,(B,C là các tiếp điểm ) .Gọi am là một điểm di động trên cung nhỏ BC (M khác B và C ) .Đường thẳng AM cắt (O) tại điểm thứ 2 là N .Gọi E là trung điểm của MN
1, chứng minh 4 điểm A,B,O,E cùng thuộc một đường tròn .Xác định tâm của đường tròn đó
2, chứng minh 2 góc BNC +góc BAC = 180 độ
3, chứng minh AC bình (mũ 2) =AM.AN và MN bình (mũ 2) =4(AE bình -AC bình )
4, gọi I ,J lần lượt là hình chiếu của M trên cạnh AB ,AC .Xác định vị trí của M sao cho tích MI.MJ đạt giác trị lớn nhất