Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SBC là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy, biết \(\alpha\) là góc giữa đường thẳng SD và (SBC) và \(\sin\alpha=\frac{2\sqrt{26}}{13}\) . Gọi \(\beta\) là góc giữa hai mặt phẳng (SAC) và (ABCD). Tính \(\beta\) ?
Mong mọi người hướng dẫn giải! Cám ơn mọi người!





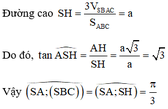
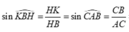
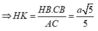
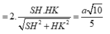
S D A B C H K O
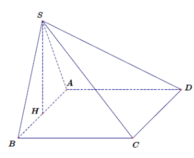
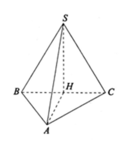
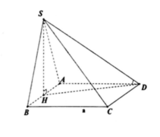
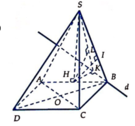
\(\left\{{}\begin{matrix}\left(SBC\right)\perp\left(ABCD\right)\\\left(SBC\right)\cap\left(ABCD\right)=BC\\CD\perp BC\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SBC\right)\Rightarrow\alpha=\widehat{DSC}\)
Đặt cạnh đáy là \(x\Rightarrow SD=\frac{x}{sin\alpha}=\frac{x\sqrt{26}}{4}\)
\(\Rightarrow SC=\sqrt{SD^2-CD^2}=\frac{x\sqrt{10}}{4}\)
Gọi H là trung điểm BC \(\Rightarrow SH\perp\left(ABCD\right)\)
Từ H kẻ \(HK\perp AC\Rightarrow\widehat{SKH}=\beta\)
\(SH=\sqrt{SC^2-\left(\frac{BC}{2}\right)^2}=\frac{x\sqrt{6}}{4}\)
\(HK=\frac{1}{2}BO=\frac{1}{4}BD=\frac{x\sqrt{2}}{4}\)
\(\Rightarrow tan\beta=\frac{SH}{HK}=\sqrt{3}\Rightarrow\beta=60^0\)