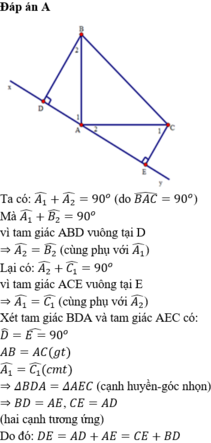
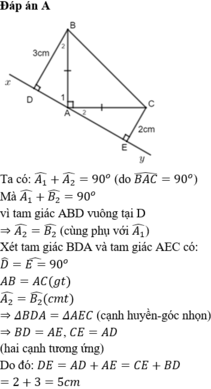
Bài 1: Cho tam giác ABC vuông tại A. Qua A kẻ đường thẳng xy sao cho xy tạo với AB góc BAx = 45 độ( Góc BAx nằm ngoài tam giác ABC). Từ B và C hạ BK vuông góc với xy, CI vuông góc với xy, M là trung điểm của BC. Chứng minh:
a) MI và MK lần lượt là trung trực của AC và AB
b) Góc IMK vuông
Bài 2: Cho tam giác ABC có góc A tù. Tia phân giác của góc B và góc C cắt nhau tại O. Lấy điểm E trên cạnh AB. Từ E hạ EP vuông góc với BO và từ P hạ PF vuông góc với OC( P thuộc BC và F thuộc AC). Chứng minh rằng: Khi E di động trên cạnh AB thì đường trung trực của EF luôn đi qua 1 điểm cố định