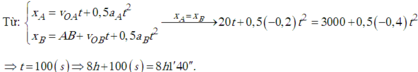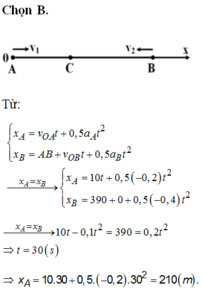Bài 44. Cùng một lúc, một ôtô chuyển động chậm dần đều qua điểm A về phía điểm B với
tốc độ 25 m/s, gia tốc có độ lớn 0,5 m/s 2 và một xe máy bắt đầu chuyển động nhanh dần đều
từ điểm B về phía A với gia tốc có độ lớn 1,5 m/s 2 . Cho AB = 100 m.
a. Viết phương trình chuyển động của hai xe.
b. Xác định vị trí và thời điểm hai xe gặp nhau.
c. Xác định vận tốc của hai xe lúc gặp nhau.
d. Xác định khoảng cách giữa hai xe sau khi khảo sát 10 s.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc tọa độ tại A.
Chiều dương từ A đến B.
Gốc thời gian lúc khởi hành.
Lúc \(t_0=0\)
Xe 1 : \(x_{01}=0;v_{01}=+7,2km/h=+2m/s;a_1=+0,4m/s^2\)
Xe 2 : \(x_{02}=240m;v_{02}=-36km/h=-10m/s;a_2=+0,4m/s^2\)
\(a,PTCD\) của 2 xe : \(x=\dfrac{1}{2}at^2+v_0t+x_0\)
Xe 1 : \(x_1=\dfrac{1}{2}.0,4.t^2+2t+0\\ x_1=\dfrac{1}{5}t^2+2t\left(m;s\right)\)
Xe 2 : \(x_2=\dfrac{1}{2}.0,4.t^2+\left(-10\right).t+240\\ x_2=\dfrac{1}{5}t^2-10t+240\left(m;s\right)\)
Vậy phương trình chuyển động của 2 xe lần lượt là \(x_1=\dfrac{1}{5}t^2+2t\left(m;s\right),x_2=\dfrac{1}{5}t^2-10t+240\left(m;s\right)\)
\(b,\) Khi 2 xe gặp nhau thì : \(x_1=x_2\)
\(\Leftrightarrow\dfrac{1}{5}t^2+2t=\dfrac{1}{5}t^2-10t+240\\ \Leftrightarrow t=20\left(s\right)\)
Thay \(t=20\) vào \(x_1=\dfrac{1}{5}.20^2+2.20=120\left(m\right)\)
Vậy 2 xe gặp nhau sau \(20s\) kể từ lúc xuất phát, vị trí gặp nhau cách A \(120m\).