cho tam giác ABC vuông tại A, vẽ AH vuông góc với BC(H thuộc BC) Vẽ tia phân giác AD của tam giác ABH(D thuộc BH) Vẽ HK song song với AD (K thuộc AC) Chứng minh rằng tam giác CHK có hai góc bằng nhau
GIÚP MK VS NHOA, THANKS NHÌU!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 7 2017
a) Xét \(\Delta ADH\)vuông tại H có \(\widehat{ADH}=90^0-\widehat{DAH}\) (1)
Mà \(\widehat{DAH}=\widehat{BAD}\) ( vì AD là tia phân giác của\(\widehat{BAH}\))
\(\Rightarrow\widehat{ADH}=90^0-\widehat{BAD}\). Mà \(90^0-\widehat{BAD}=\widehat{DAC}\)(2)
Từ ( 1 ) và ( 2 ) \(\Rightarrow\widehat{ADH}=\widehat{DAC}\)
\(\Rightarrow\Delta CAD\)cân tại C
b) Vì \(\Delta CAD\)cân tại C ( cm ở ý a )\(\Rightarrow\widehat{CAD}=\frac{180^0-\widehat{C}}{2}\)( *)
Ta có :\(CH=CK\Rightarrow\Delta CHK\)cân tại C \(\Rightarrow\widehat{CKH}=\frac{180^0-\widehat{C}}{2}\)(**)
Từ (*) và (**) \(\Rightarrow\widehat{CAD}=\widehat{CKH}\)
Mà \(\widehat{CAD}\)và\(\widehat{CKH}\)là 2 góc đồng vị
\(\Rightarrow\)AD song song HK
13 tháng 7 2023
a: Xét ΔABH vuông tại H và ΔKIH vuông tại H có
HA=HK
HB=HI
=>ΔABH=ΔKIH
b: ΔABH=ΔKIH
=>góc ABH=góc KIH
=>AB//IK
c: IK//AB
AB vuông góc AC
=>IK vuông góc AC
=>I,K,E thẳng hàng
d: Xét tứ giác ABKI có
H là trung điểm chung của AK và BI
AK vuông góc BI
=>ABKI là hình thoi
=>AB=AI=IK
=>IK=ID
=>góc IKD=góc IDK
KV
16 tháng 12 2023
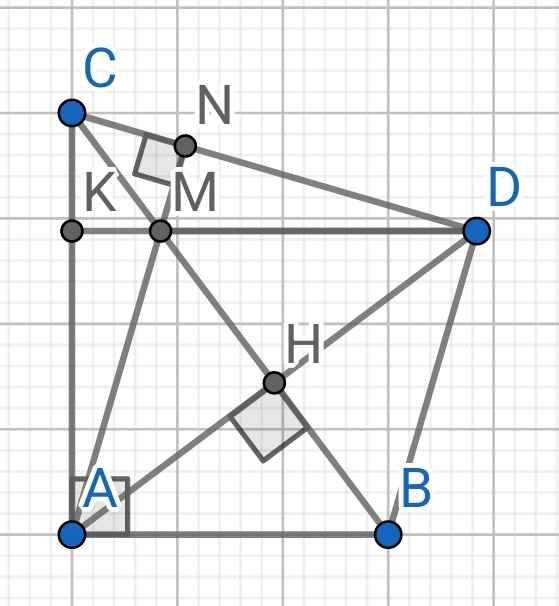a) Sửa đề: Chứng minh ABH = DBH
Giải:
Xét hai tam giác vuông: ∆ABH và ∆DBH có:
BH là cạnh chung
AH = DH (gt)
⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)
⇒ ∠ABH = ∠DBH (hai góc tương ứng)
⇒ BH là tia phân giác của ∠ABD
b) Do DM // AB (gt)
⇒ ∠MDH = ∠HAB (so le trong) (1)
Do ∆ABH = ∆DBH (cmt)
⇒ ∠HAB = ∠HDB (hai góc tương ứng) (2)
Từ (1) và (2) ⇒ ∠MDH = ∠HDB
Xét hai tam giác vuông: ∆DHM và ∆DHB có:
DH là cạnh chung
∠MDH = ∠HDB (cmt)
⇒ ∆DHM = ∆DHB (cạnh góc vuông - góc nhọn kề)
⇒ ∠DHM = ∠DHB (hai góc tương ứng)
Mà ∠DHM + ∠DHB = 180⁰ (kề bù)
⇒ ∠DHM = ∠DHB = 180⁰ : 2 = 90⁰
⇒ DH ⊥ BM (3)
Do ∆DHM = ∆DHB (cmt)
⇒ HM = HB
⇒ H là trung điểm của BM (4)
Từ (3) và (4) ⇒ HD là đường trung trực của BM
⇒ AD là đường trung trực của BM
c) Do AD là đường trung trực của BM (cmt)
⇒ AD ⊥ CH
Do DK // AB (gt)
⇒ DK ⊥ AC (AB ⊥ AC)
∆ACD có:
CH là đường cao (CH ⊥ AD)
DK là đường cao thứ hai (DK ⊥ AC)
⇒ AM là đường cao thứ ba
Mà AM ⊥ CN tại N
⇒ AN là đường cao thứ ba của ∆ACD
⇒ C, N, D thẳng hàng
24 tháng 6 2023
góc ABE=góc HBE=60/2=30 độ
=>góc AEB=góc HEB=60 độ
=>góc AEH=120 độ
HK//BE
=>góc KHE=góc HEB=60 độ
góc KEH=180-120=60 độ
Xét ΔKEH có góc KHE=góc KEH=60 độ
nên ΔKEH đều
7 tháng 4 2020
Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
LA
8 tháng 4 2020
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A