cho hàm số:
y=1/2x\(^2\)
1) Nêu tập xác định , chiều biến thiên và vẽ đồ thị của hàm số
2) Lập phương trình đướng thẳng đi qua điểm (2;-6)có hệ số góc a và tiếp xúc với đồ thị hàm số trên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 12 2021
a: \(\left\{{}\begin{matrix}x_I=\dfrac{3}{2\cdot1}=\dfrac{3}{2}\\y_I=-\dfrac{\left(-3\right)^2-4\cdot1\cdot\left(-2\right)}{4\cdot1}=-\dfrac{17}{4}\end{matrix}\right.\)
30 tháng 7 2023
a: Thay x=-1 và y=1 vào (d), ta được:
-(2m+1)=1
=>2m+1=-1
=>2m=-2
=>m=-1
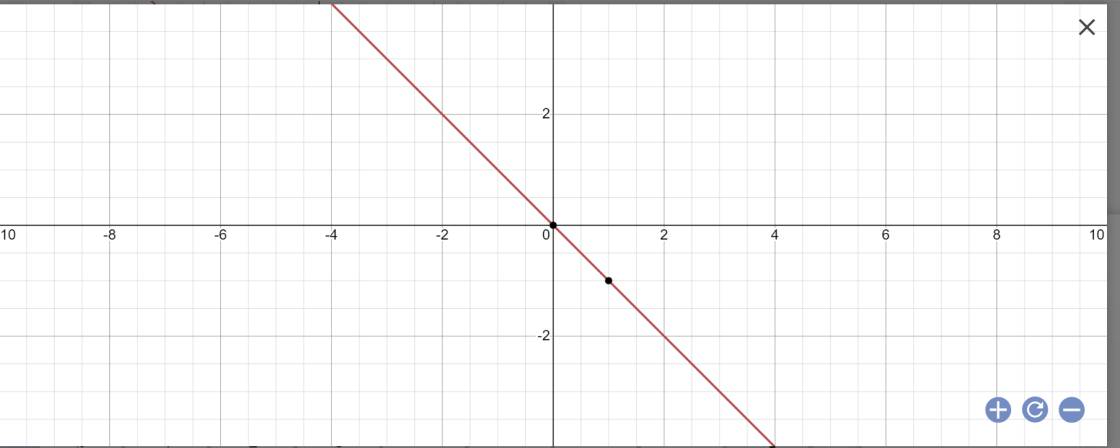
b: y=(-2+1)x=-x
4 tháng 12 2021
\(a,\Leftrightarrow1+m=-2\Leftrightarrow m=-3\\ \Leftrightarrow y=x-3\\ \text{Thay }x=2;y=5\Leftrightarrow5=2-3=-1\left(\text{vô lí}\right)\\ \Leftrightarrow E\notinđths\\ b,\text{PT giao Ox và Oy: }\left\{{}\begin{matrix}y=0\Rightarrow x=-m\Rightarrow E\left(-m;0\right)\Rightarrow OE=\left|m\right|\\x=0\Rightarrow y=m\Rightarrow F\left(0;m\right)\Rightarrow OF=\left|m\right|\end{matrix}\right.\)
Gọi H là chân đường cao từ O đến EF
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OE^2}+\dfrac{1}{OF^2}=\dfrac{1}{2m^2}=\dfrac{1}{3^2}=\dfrac{1}{9}\)
\(\Leftrightarrow m^2=\dfrac{9}{2}\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{\sqrt{2}}\\m=-\dfrac{3}{\sqrt{2}}\end{matrix}\right.\)
L
11 tháng 1 2020
a) Đths \(y=\left(2m+1\right)x\) đi qua \(A\left(-1;1\right)\)
Ta có:
\(y=\left(2m+1\right)x\)
\(\Rightarrow\left(2m+1\right)\left(-1\right)=1\)
\(\Rightarrow2m+1=-1\)
\(\Rightarrow2m=-2\)
\(\Rightarrow m=-1\)
b) Thay \(m=-1\)
\(\Rightarrow y=\left(-2+1\right)x\)
\(\Rightarrow y=-x\)
Lập bảng giá trị:
| \(x\) | \(0\) | \(-2\) |
| \(y=-x\) | \(0\) | \(2\) |
13 tháng 2 2022
a: Vì (d)//y=2x+3 nên a=2
Vậy: y=2x+b
Thay x=1 và y=-2 vào (d), ta được:
b+2=-2
hay b=-4
Vậy: (d): y=2x-4
c: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-4x+3=2x-4\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{6}\\y=-\dfrac{5}{3}\end{matrix}\right.\)
d: Vì hai đường song song nên 2m-3=2
=>2m=5
hay m=5/2