Bài 1: Hãy xác định các tập hợp sau bằng cách liệt kê các phần tử của tập hợp đó:
a) A = {x ∈ N* | x < 8}
b) C = {x ∈ N | x chia hết cho 6 và 37 < x < 54}
Bài 2:
a) Viết tập hợp A các số tự nhiên lớn hơn 4 và không vượt quá 7 bằng hai cách.
b) Tập hợp các số tự nhiên khác 0 và không vượt quá 12 bằng hai cách.
Bài 3: Hãy tính số phần tử của các tập hợp sau:
a) Tập hợp A các số tự nhiên lẻ có bốn chữ số.
b) Tập hợp B các số tự nhiên chẵn có ba chữ số.
Dạng 2: TÍNH HỢP LÝ
Bài 4: Thực hiện phép tính:
a) 3.52 + 15.22 – 26:2 b) 2021 + 5[300 – (17 – 7)2] c) 32.5 + 23.10 – 81:3 | d) (519 : 517 + 3) : 7 e) -(34-97%2B228)-2021%5E%7B0%7D) f) 128.46 + 128.32 + 128.22 |
Dạng 3: TÌM X
Bài 5: Tìm x, biết
a) 165 : x = 3 b) x – 71 = 129 c) 9x- 1 = 9 | d) 32(x + 4) – 52 = 5.22 e) 135 – 5(x + 4) = 35 f) x4 = 16 |
Dạng 4: DẤU HIỆU CHIA HẾT - BỘI VÀ ƯỚC
Bài 6: Tìm các chữ số x và y sao cho
a) Số 17x chia hết cho cả 2 và 3.
b) Số x45y chia hết cho cả 2; 5; 3 và 9.
Bài 7: Tìm x, biết:
1) 24 ⋮ x; 36 ⋮ x ; 150 ⋮ x và x lớn nhất. 3) x ∈ ƯC(54 ; 12) và x > -10 | 2) x ∈ BC(6; 4) và 16 ≤ x ≤50. 4) x ⋮ 4; x ⋮ 5; x ⋮ 8 và -20 < x < 180 |
Bài 8: Tìm ƯCLN, BCNN của
a) 12 và 18
b) 24; 36 và 60
Dạng 5: TOÁN ĐỐ
Bài 9: Học sinh khối 6 có 195 nam và 117 nữ tham gia lao động. Thầy phụ trách muốn chia ra thành các tổ sao cho số nam và nữ mỗi tổ đều bằng nhau. Hỏi có thể chia nhiều nhất mấy tổ? Mỗi tổ có bao nhiêu nam, bao nhiêu nữ?
Bài 10: Tìm số học sinh khối 6 của một trường biết rằng khi xếp thành các tổ có 36 hoặc 90 học sinh đều vừa đủ, số học sinh khối 6 nằm trong khoảng từ 300 đến 400 em.
Bài 11: Ngoan, Lễ, Độ đang trực nhật chung với nhau ngày hôm nay là thứ hai. Biết rằng Ngoan cứ 4 ngày trực nhật một lần, Lễ 8 ngày trực một lần, Độ 6 ngày trực một lần. Hỏi sau ít nhất mấy ngày thì Ngoan, Lễ, Độ lại trực chung lần tiếp theo? Đó là vào ngày thứ mấy trong tuần?
Đề cương ôn tập học kì 1 Toán 6 Kết nối tri thức
I. BÀI TẬP TRẮC NGHIỆM
Bài 1: Khoanh tròn vào chữ cái trước câu trả lời đúng:
Câu 1: Ba số nào sau đây là ba số tự nhiên liên tiếp tăng dần:
A. b – 1; b; b + 1 (b ∈ N).
B. b; b + 1; b + 2 (b∈ N).
C. 2b; 3b; 4b (b ∈ N).
D. b + 1; b; b - 1 (b ∈N)..
Câu 2: Giá trị của tổng  là:
là:
A. 5050.
B. 2500.
C. 5000.
D. 2450.
Câu 3: Kết quả của phép tính  bằng:
bằng:
A. 5.
B. 58
C. 57
D. 56
Câu 4: Biết ![\left[(x-3)^{2}+7\right] \cdot 2=14](https://tex.vdoc.vn/?tex=%5Cleft%5B(x-3)%5E%7B2%7D%2B7%5Cright%5D%20%5Ccdot%202%3D14) . Vậy giá trị của là:
. Vậy giá trị của là:
A. x = 0.
B. x = 3.
C. x = 7.
D. x = 3 và x = 7.
Câu 5: Cho số  chữ số thích hợp để M chia hết là:
chữ số thích hợp để M chia hết là:
A. 2.
B. 8.
C. 4.
D. 5.
Ngoài ra các bạn học sinh có thể tham khảo chuyên mục sách mới chương trình GDPT:
Toán lớp 6
Kết nối tri thứcToán lớp 6
Cánh DiềuToán lớp 6
Chân Trời Sáng TạoC. Đề cương ôn tập học kì 1 lớp 6 môn Toán sách cũI. PHẦN SỐ HỌC:
* Chương I:
Tập hợp: cách ghi một tập hợp; xác định số phần tử của tập hợpCác phép tính cộng, trừ, nhân, chia số tự nhiên;đề cương ôn tập học kì 1 toán 6 các công thức về lũy thừa và thứ tự thực hiện phép tínhTính chất chia hết của một tổng và các dấu hiệu chia hết cho 2, 3, 5, 9Phân tích một số ra thừa số nguyên tốCách tìm ƯCLN, BCNN* Chương II:
Thế nào là tập hợp các số nguyên.Thứ tự trên tập số nguyênQuy tắc: Cộng hai số nguyên cùng dấu, cộng hai số nguyên khác dấu, trừ hai số nguyên, quy tắc dấu ngoặc, quy tắc chuyển vế.Tham khảo bộ đề thi học kì 1 mới nhất: Bộ đề thi học kì 1 lớp 6 môn Toán
II. PHẦN HÌNH HỌC
1. Thế nào là điểm, đoạn thẳng, tia?
2. Khi nào ba điểm A, B, C thẳng hàng?
3. Khi nào thì điểm M là điểm nằm giữa đoạn thẳng AB?
- Trung điểm M của đoạn thẳng AB là gì?
4. Thế nào là độ dài của một đoạn thẳng?
- Thế nào là hai tia đối nhau? Trùng nhau? Vẽ hình minh hoạ cho mỗi trường hợp.
5. Cho một ví dụ về cách vẽ:
Đoạn thẳng.Đường thẳng.Tia.Trong các trường hợp cắt nhau; trùng nhau, song song?
D. Đề cương ôn tập học kì 1 lớp 6 môn Toán Dạng bài tập tự luậnI. TẬP HỢP
Bài 1:
a. Viết tập hợp A các số tự nhiên lớn hơn 4 và không vượt quá 7 bằng hai cách.
b. Tập hợp các số tự nhiên khác 0 và không vượt quá 12 bằng hai cách.
c. Viết tập hợp M các số tự nhiên lớn hơn hoặc bằng 11 và không vượt quá 20 bằng hai cách.
d. Viết tập hợp M các số tự nhiên lớn hơn 9, nhỏ hơn hoặc bằng 15 bằng hai cách.
e. Viết tập hợp A các số tự nhiên không vượt quá 30 bằng hai cách.
f. Viết tập hợp B các số tự nhiên lớn hơn 5 bằng hai cách.
g. Viết tập hợp C các số tự nhiên lớn hơn hoặc bằng 18 và không vượt quá 100 bằng hai cách.
Bài 2: Viết Tập hợp các chữ số của các số:
a) 97542
b) 29635
c) 60000
Bài 3: Viết tập hợp các số tự nhiên có hai chữ số mà tổng của các chữ số là 4.
Bài 4: Viết tập hợp sau bằng cách liệt kê các phần tử.
a) A = {x ∈ N | 10 < x <16} b) B = {x ∈ N | 10 ≤ x ≤ 20 c) C = {x ∈ N | 5 < x ≤ 10} | d) D = {x ∈ N | 10 < x ≤ 100} e) E = {x ∈ N | 2982 < x <2987} f) F = {x ∈ N* | x < 10} | g) G = {x ∈ N* | x ≤ 4} h) H = {x ∈ N* | x ≤ 100} |
Bài 5: Cho hai tập hợp A = {5; 7}, B = {2; 9}
Viết tập hợp gồm hai phần tử trong đó có một phần tử thuộc A, một phần tử thuộc B.
Bài 6: Viết tập hợp sau và cho biết mỗi tập hợp có bao nhiêu phần tử
a. Tập hợp các số tự nhiên khác 0 và không vượt quá 50.
b. Tập hợp các số tự nhiên nhỏ hơn 100.
c. Tập hợp các số tự nhiên lớn hơn 23 và nhỏ hơn hoặc bằng 1000.
d. Các số tự nhiên lớn hơn 8 nhưng nhỏ hơn 9.
>> Đề thi mới nhất: Đề thi học kì 1 môn Toán lớp 6
II. THỰC HIỆN PHÉP TÍNH
Bài 1: Thực hiện phép tính:
a) 3. 52 + 15. 22 – 26:2 b) 53. 2 – 100 : 4 + 23. 5 c) 62 : 9 + 50. 2 – 33. 3 d) 32. 5 + 23. 10 – 81:3 e) 513 : 510 – 25. 22 f) 20 : 22 + 59 : 58 g) 100 : 52 + 7. 32 h) 84 : 4 + 39 : 37 + 50 i) 29 – [16 + 3. (51 – 49)] | j) (519 : 517 + 3) : 7 k) 79 : 77 – 32 + 23. 52 l) 1200 : 2 + 62. 21 + 18 m) 59 : 57 + 70 : 14 – 20 n) 32. 5 – 22. 7 + 83 o) 59 : 57 + 12. 3 + 70 p) 5. 22 + 98 : 72 q) 311 : 39 – 147 : 72 r) 295 – (31 – 22. 5)2 | s) 151 – 291 : 288 + 12. 3 t) 238 : 236 + 51. 32 - 72 u) 791 : 789 + 5. 52 – 124 v) 4. 15 + 28:7 – 620 : 618 w) (32 + 23. 5) : 7 x) 1125 : 1123 – 35 : (110 + 23) – 60 y) 520 : (515. 6 + 515. 19) z) 718 : 716 +22. 33 aa) 59. 73 - 302 + 27. 59 |
Bài 2: Thực hiện phép tính:
a) 47 – [(45. 24 – 52. 12):14] b) 50 – [(20 – 23) : 2 + 34] c) 102 – [60 : (56 : 54 – 3. 5)] d) 50 – [(50 – 23. 5):2 + 3] e) 10 – [(82 – 48). 5 + (23. 10 + 8)] : 28 f) 8697 – [37 : 35 + 2(13 – 3)] g) 2011 + 5[300 – (17 – 7)2] h) 695 – [200 + (11 – 1)2] i) 129 – 5[29 – (6 – 1)2] j) 2010 – 2000 : [486 – 2(72 – 6)] | k) 2345 – 1000 : [19 – 2(21 – 18)2] l) 128 – [68 + 8(37 – 35)2] : 4 m) 568 – {5[143 – (4 – 1)2] + 10} : 10 n) 107 – {38 + [7. 32 – 24 : 6+(9 – 7)3]}:15 o) 307 – [(180 – 160) : 22 + 9] : 2 p) 205 – [1200 – (42 – 2. 3)3] : 40 q) 177 :[2. (42 – 9) + 32(15 – 10)] r) [(25 – 22. 3) + (32. 4 + 16)]: 5 s) 125(28 + 72) – 25(32. 4 + 64) t) 500 – {5[409 – (23. 3 – 21)2] + 103} : 15 |



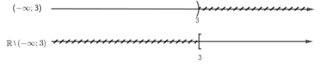






R\(-1;+∞)=(-∞;-1]
R\[0;2)=(-∞;0)\(\cup\)[2;+∞)