chọn bất kỳ n+1 số trong 2n số tự nhiên từ 1 đến 2n ( n>1) chứng minh rằng trong các số đc chọn có ít nhất 1 số bằng tổng của 2 số đc chọn ( kể cả các truowgf hợp số hạng của tổng bằng nhau )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 12 2017
Số có 4 chữ số có dạng 
Số phần tử của không gian mẫu: n(S)=9.9.8.7=4536.
Gọi A: “ tập hợp các số tự nhiên có 4 chữ số phân biệt và lớn hơn 2500.”
TH1: a>2
Chọn a: có 7 cách chọn.
Chọn b: có 9 cách chọn.
Chọn c: có 8 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có:7.9.8.7=3528 .
TH2: a=3; b>5
Chọn a: có 1 cách chọn.
Chọn b: có 4 cách chọn.
Chọn c: có 8cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.4.8.7=224 (số).
TH3: a=2; b=5; c>0
Chọn a: có 1 cách chọn.
Chọn b: có1 cách chọn.
Chọn c: có 7 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.1.7.7=49(số).
TH4. a=2; b=5; c=0 ;d>0
Chọn a: có 1 cách chọn.
Chọn b: có 1 cách chọn.
Chọn c: có 1 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.1.1.7=7(số).
Như vậy: n(A)=3528+224+49+7=3808
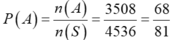
Chọn C.
3 tháng 5 2016
Bài này ta chỉ cần chứng minh có 4 số khác nhau trong 2002 số là được
Giả sử có 5 số khác nhau thì có 5 số a_1<a_2<a_3<a_4<a_5
Theo đề bài ta có
Xét 4 số a1;a2;a3;a4
a1.a4=a2.a3(ko thể có a1.a2=a3.a4 hay a1.a3=a2.a4) (1)
Xét 4 số a1;a2;a3;a5
a1.a5=a2.a3 (2)
Từ (1) và (2) suy ra a4=a5(không thỏa mãn)
Suy ra chỉ có 4 số khác nhau trong đó
Từ có 4 số khác nhau thì việc suy ra có 501 số bằng nhau quá dễ dàng
TA
27 tháng 9 2020
1) Số lớn nhất : 20000 , số nhỏ nhất : 10001
2) Đáp số : 999995 .
3 tháng 8 2023
\(a)\) Công thức tính số hạng của một dãy số là : (Số cuối-số đầu ) chia khoảng cách rồi cộng thêm 1 .
Do đó : Số hạng của dãy số A là : \(\dfrac{\left(2n+1\right)-1}{2}+1=n+1\)
Số hạng của dãy số B là : \(\dfrac{2n-2}{2}+1=n-1+1=n\)
\(b)\) Ta có : Số hạng của dãy số A là : \(n+1\)
Do đó : tổng của A là : \(\dfrac{\left(2n+1+1\right).\left(n+1\right)}{2}=\dfrac{2\left(n+1\right)\left(n+1\right)}{2}\)
\(=\left(n+1\right)^2\)
Vì n thuộc N nên tổng của A là : một số chính phương .
\(c)\) Ta có : Số hạng của dãy số B là : n
Do đó : Tổng của dãy số B là : \(\dfrac{n.\left(2n+2\right)}{2}=\dfrac{2.n.\left(n+1\right)}{2}\)
\(=n.\left(n+1\right)\)
Ta thấy : n(n+1) là tích của 2 số tự nhiên liên tiếp nên để B là số chính phương thì khi và chỉ khi n hoặc n+1 bằng 0 .
Ta thấy chúng đều không thoả mãn .
vậy.............