Trong tất cả các hình chữ nhật có chiều dài đường chéo không đổi d, hãy tìm hình có diện tích lớn nhất?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
7 tháng 1 2018
Gọi x,y là kích thước của hình chữ nhật (x,y>0)
ta có: x2+y2=d2(đl pytago)
Từ (x-y)2>= 0 suy ra x2-2xy+y2>=0 suy ra x2+y2>= 2xy
Ta có xy<= d2/2, không đổi.
dấu ''='' xảy ra <=> x=y
suy ra ABCD là hình vuông
Vậy trong tất cả các hình chữ nhật có chiều dài đường chéo d không đổi thì hình vuông có diện tích lớn nhất và bằng d2/2
CM
3 tháng 8 2017
Gọi các kích thước của hình hộp lần lượt là a, b, c (a, b, c > 0)
Theo đề bài ta có a2 + b2 + c2= d2
Diện tích toàn phần của hình hộp là:
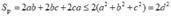
Dấu "=" xảy ra Û a = b = c.
Vậy hình hộp có diện tích toàn phần lớn nhất là hình lập phương.
HN
1
19 tháng 9 2021
Gọi x,y là kích thước của hình chữ nhật (x,y>0)
ta có: x2+y2=d2(đl pytago)
Từ (x-y)2>= 0 suy ra x2-2xy+y2>=0 suy ra x2+y2>= 2xy
Ta có xy<= d2/2, không đổi.
dấu ''='' xảy ra <=> x=y
suy ra ABCD là hình vuông
Vậy trong tất cả các hình chữ nhật có chiều dài đường chéo d không đổi thì hình vuông có diện tích lớn nhất và bằng \(\frac{8\sqrt{2}}{2}=4\sqrt{2}\)
LH
0
CM
10 tháng 3 2019
Đáp án B
Giả độ dài các cạnh của khối hộp lần lượt là a; b; c khi đó T = 2ab + 2bc + 2ca = 36.
⇔ a b + b c + c a = 18 . Mặt khác A C ' = A B 2 + A D 2 + A A ' 2 = a 2 + b 2 + c 2 = 6
Khi đó a 2 + b 2 + c 2 = 36 a b + b c + c a = 18 ⇒ a + b + c 2 = 72 a b + b c + c a = 18 ⇔ a + b + c = 6 2 b a + c + a c = 18
Ta có: V = a b c = b . 18 - b a + c = b 18 - b 6 2 - b = b 3 - 6 2 b 2 + 18 b = f b
Xét f b = b 3 - 6 2 b 2 + 18 b , 0 < b < 6 2 ta có : f ' b = 3 b 2 - 12 2 b + 18 = 0 ⇔ b 2 - 4 b 2 + 6 = 0
⇔ [ b = 3 2 b = 3 ⇒ f 3 2 = 0 ; f 2 = 8 2 ⇒ M a x ( 0 ; 6 2 ) f b = 8 2 .
1 tháng 5 2016
Nửa chu vi là:
92 : 2 = 46 ( m )
Chiều dài là:
( 46 + 10 ) : 2 = 28 ( m )
Chiều rộng là:
28 - 10 = 18 ( m )
Diện tích hình thoi là:
28 x 18 : 2 = 252 ( m2)
Đáp số: 252 m2
1 tháng 5 2016
nửa chu vi : 92 : 2 = 46 (m)
chiều dài : (46 + 10) : 2 = 28 (m)
chiều rộng : 28 - 10 = 18 (m)
diện tích hình thoi : 28 x 18 : 2 = 252 (m2)
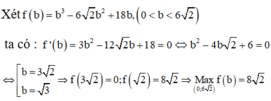
Gọi x,y là kích thước của hình chữ nhật (x,y>0)
ta có: x2+y2=d2(đl pytago)
Từ (x-y)2>= 0 suy ra x2-2xy+y2>=0 suy ra x2+y2>= 2xy
Ta có xy<= d2/2, không đổi.
dấu ''='' xảy ra <=> x=y
suy ra ABCD là hình vuông
Vậy trong tất cả các hình chữ nhật có chiều dài đường chéo d không đổi thì hình vuông có diện tích lớn nhất và bằng d2/2