Giải phương trình
2x(8x-1)2 (4x-1)=9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




⇔ 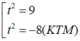
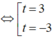
Với t = 3 ⇒ x = - 1/2
Với t = - 3 ⇒ x = - 5/4
Vậy tập nghiệm của phương trình là S = { - 1/2; - 5/4 }

\(2x\left(8x-1\right)^2\left(4x-1\right)=9\)
\(\Leftrightarrow8x\left(8x-1\right)^2\left(8x-2\right)=72\)(nhân hai vế với 8)
Đặt \(8x-1=y\). Khi đó, pt được viết lại:
\(\left(y+1\right)y^2\left(y-1\right)=72\)
\(\Leftrightarrow y^2\left(y^2-1\right)=72\)
\(\Leftrightarrow y^4-y^2-72=0\)
\(\Leftrightarrow y^4+3y^3-3y^3-9y^2+8y^2+24y-24y-72=0\)
\(\Leftrightarrow y^3\left(y+3\right)-3y^2\left(y+3\right)+8y\left(y+3\right)-24\left(y+3\right)=0\)
\(\Leftrightarrow\left(y+3\right)\left(y^3-3y^2+8y-24\right)=0\)
\(\Leftrightarrow\left(y+3\right)\left(y^2\left(y-3\right)+8\left(y-3\right)\right)=0\)
\(\Leftrightarrow\left(y+3\right)\left(y-3\right)\left(y^2+8\right)=0\)
Mà \(y^2+8\ge8>0\)
\(\Rightarrow\orbr{\begin{cases}y+3=0\\y-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}y=-3\\y=3\end{cases}}}\)
TH1: \(y=-3\)
\(\Rightarrow8x-1=-3\)
\(\Leftrightarrow8x=-2\)
\(\Leftrightarrow x=\frac{-1}{4}\)
TH2: \(y=3\)
\(\Rightarrow8x-1=3\)
\(\Leftrightarrow8x=4\)
\(\Leftrightarrow x=\frac{1}{2}\)
Vậy tập nghiệm của pt là S={\(\frac{-1}{4};\frac{1}{2}\)}


a)2x(8x-1)2 (4x-1)=9
\(\Leftrightarrow\text{ (64x}^2\text{-16x+1)(8x}^2\text{-2x)=9}\)
\(\Leftrightarrow\text{ 512x}^4\text{-256x}^3\text{+40x}^2\text{-2x=9}\)
\(\Leftrightarrow\text{ 512x}^4\text{-256x}^3\text{+40x}^2\text{-2x-9=0}\)
\(\Leftrightarrow\text{ 512x}^4\text{-128x}^3\text{-64x}^2\text{-128x}^3\text{+32x}^2\text{+16x+72x}^2\text{-18x-9=0}\)
\(\Leftrightarrow\text{ (512x}^4\text{-128x}^3\text{-64x}^2\text{)-(128x}^3\text{-32x}^2\text{-16x)+(72x}^2\text{-18x-9)=0}\)
\(\Leftrightarrow\text{ 64x}^2\text{(8x}^2\text{-2x-1)-16x(8x}^2\text{-2x-1)+9(8x}^2\text{-2x-1)=0}\)
\(\Leftrightarrow\text{ (64x}^2\text{-16x+9)(8x}^2\text{-2x-1)=0}\)
\(\Leftrightarrow\text{ (64x}^2\text{-16x+9)(8x}^2\text{-4x+2x-1)=0}\)
\(\Leftrightarrow\text{ (64x}^2\text{-16x+9)(2x-1)(4x+1)=0}\)
\(\Rightarrow\left\{{}\begin{matrix}2x-1=0\\4x+1=0\end{matrix}\right.\) (Vì 64x2 -16x+9 =0 )
\(\Rightarrow\left\{{}\begin{matrix}x=\frac{1}{2}\\x=-\frac{1}{4}\end{matrix}\right.\)

Ta có : \(2x\left(8x-1\right)^2\left(4x-1\right)=9\)
=> \(\left(8x^2-2x\right)\left(64x^2-16x+1\right)=9\)
=> \(512x^4-128x^3+8x^2-128x^3+32x^2-2x-9=0\)
=> \(512x^4-256x^3+40x^2-2x-9=0\)
=> \(512x^4+128x^3-384x^3-96x^2+136x^2+34x-36x-9=0\)
=> \(128x^3\left(4x+1\right)-96x^2\left(4x+1\right)+34x\left(4x+1\right)-9\left(4x+1\right)=0\)
=> \(\left(4x+1\right)\left(128x^3-96x^2+34x-9\right)=0\)
=> \(\left(4x+1\right)\left(128x^3-64x^2-32x^2+16x+18x-9\right)=0\)
=> \(\left(4x+1\right)\left(64x^2\left(2x-1\right)-16x\left(2x-1\right)+9\left(2x-1\right)\right)=0\)
=> \(\left(4x+1\right)\left(2x-1\right)\left(64x^2-16x+9\right)=0\)
Ta thấy : \(64x^2-16x+9\)
\(=\left(64x^2-2.8.x+1\right)+8\)
\(=\left(8x-1\right)^2+8>0\)
=> \(\left(4x+1\right)\left(2x-1\right)=0\)
=> \(\left[{}\begin{matrix}4x+1=0\\2x-1=0\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=-\frac{1}{4}\\x=\frac{1}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là \(S=\left\{-\frac{1}{4};\frac{1}{2}\right\}\)

1: \(\Leftrightarrow\left(x-4\right)^2+14=-9\left(x-4\right)\)
\(\Leftrightarrow x^2-8x+16+14+9x-36=0\)
\(\Leftrightarrow x^2+x-6=0\)
=>(x+3)(x-2)=0
=>x=-3(nhận) hoặc x=2(nhận)
2: \(\Leftrightarrow\left(8x+1\right)\left(2x-1\right)-2x\left(2x+1\right)-12x^2+9=0\)
\(\Leftrightarrow16x^2-8x+2x-1-4x^2-2x-12x^2+9=0\)
=>-8x+8=0
hay x=1(nhận)
c: \(\dfrac{1}{2\left(x-3\right)}-\dfrac{3x-5}{\left(x-3\right)\left(x-1\right)}=\dfrac{1}{2}\)
\(\Leftrightarrow x-1-2\left(3x-5\right)=\left(x-3\right)\left(x-1\right)\)
\(\Leftrightarrow x^2-4x+3=x-1-6x+10=-5x+9\)
\(\Leftrightarrow x^2+x-6=0\)
=>(x+3)(x-2)=0
=>x=-3(nhận) hoặc x=2(nhận)

\(PT< =>8x\left(8x-1\right)^2\left(8x-2\right)=72\)
\(< =>8x\left(8x-2\right)\left(64x^2-16x+1\right)=72\)
\(< =>\left(64x^2-16x\right)\left(64x^2-16x+1\right)=72\)
Đặt \(64x^2-16x+\frac{1}{2}=t\)
\(PT< =>\left(t-\frac{1}{2}\right)\left(t+\frac{1}{2}\right)=72\)
\(< =>t^2=\frac{289}{4}\)
\(< =>\orbr{\begin{cases}t=\frac{17}{2}\\t=\frac{-17}{2}\end{cases}}\)
\(TH1:t=\frac{17}{2}\)
\(PT< =>64x^2-16x+\frac{1}{2}=\frac{17}{2}\)
\(< =>\orbr{\begin{cases}x=\frac{1}{2}\\x=\frac{-1}{4}\end{cases}}\)
\(TH2:t=\frac{-17}{2}\)
\(PT< =>64x^2-16x+\frac{1}{2}=\frac{-17}{2}\)
\(< =>64x^2-16x+9=0\)
\(< =>\left(8x-1\right)^2+8=0\left(VL\right)\)
Vậy S={1/2;-1/4}