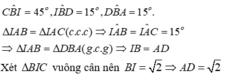Cho tam giác ABC cân tại A, góc A = 30 độ, BC = 2 cm. Trên cạnh AC lấy điểm D sao cho góc ABD=15 độ. Tính độ dài AD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 7 2018
ΔABC cân tại A mà BACˆ=300
⇒ABCˆ=ACBˆ=1800−3002=750
Từ A, kẻ AE⊥BD (E∈BD)
kẻ AF⊥BC (F∈BC)
Vì CBDˆ=600(giả thiết)
⇒ABEˆ=750−600=150
Xét ΔABE và ΔBAF có:
AFBˆ=AEBˆ(=900)
Cạnh AB chung
BAFˆ=AEBˆ(=150)
⇒ΔABE=ΔBAF (g.c.g)
⇒AE=BF=12BC=1cm
Mặt khác, trong ΔBDC có:
DBCˆ=600
DCBˆ=750
⇒BDCˆ=450
⇒BDCˆ=ADEˆ (đối đỉnh)
Mà ΔADE vuông tại E
⇒ΔADE vuông cân tại E
⇒AE=ED
Mà AE=BF=1cm (cmt)
⇒ED=1cm
Áp dụng định lí Pytago, ta có:
AD2=EA2+ED2
⇒AD2=12+12=1+1=2
⇒AD=2–√
Vậy AD=2–√
9 tháng 2 2019
Đỗ Hoài Chinh mình không hiểu chỗ AF=BF=12BC=1cm
đáng lẽ 12BC phải bằng 24cm chứ?
giải thích hộ mình nhé
KN
16 tháng 8 2016
Tam giác ABC cân tại A, có góc A bằng 30 độ, suy ra góc B và C đều bằng 75 độ
vẽ hình ra nhé, kéo dài BD
từ A hạ đường vuông góc với BD cắt BD tại E
từ A cũng hạ đường vuông góc với BC cắt BC tại F
do góc BDC = 60 độ (đề bài cho)
nên góc ABE bằng 75-60=15 độ
xét 2 tam giác ABE và ABF
- AB chung
- góc BAF = góc ABE = 15 độ
- góc AFB = góc AEB = 90 độ
suy ra 2 tam giác bằng nhau (góc - cạnh - góc)
suy ra AE = BF = 1/2 BC = 1cm
xét tam giác nhỏ ADF ta có
- tam giác này vuông tại F
- góc DAF = 45 độ
suy ra tam giác này vuông cân tại F
suy ra AD = căn 2 AF = căn 2 cm
giải thích thêm chỗ góc DAF = 45 độ
do hai tam giác lớn cm bên trên bằng nhau suy ra góc BAF = góc ABE = 75 độ
góc BAC = 30 độ (đề bài cho)
suy ra góc DAF = 45 độ
14 tháng 3 2017
\(\Delta ABC\)cân tại A nên\(\widehat{ABC}=\widehat{ACB}=\frac{180^0-\widehat{BAC}}{2}=75^0\)
Trên nửa mặt phẳng bờ BC chứa A lấy E sao cho\(\widehat{B_1}=\widehat{C_1}=45^0\)
=>\(\widehat{ABE}=75^0-45^0=30^0;\Delta EBC\)vuông cân tại E =>\(BE=EC=\frac{BC}{\sqrt{2}}=\sqrt{2}\left(cm\right)\)(định lí Pitago)
\(\Delta ABE,\Delta BAD\)có AB chung ; BE = AD\(\left(=\sqrt{2}cm\right)\);\(\widehat{ABE}=\widehat{BAD}\left(=30^0\right)\)
\(\Rightarrow\Delta ABE=\Delta BAD\left(c.g.c\right)\Rightarrow\widehat{A_1}=\widehat{B_2}\)
Lại có\(\Delta AEB=\Delta AEC\left(c.c.c\right)\)nên\(\widehat{A_1}=\widehat{A_2}=\frac{\widehat{BAC}}{2}=15^0\Rightarrow\widehat{B_2}=15^0\)
\(\Rightarrow\widehat{D_1}=\widehat{BAD}+\widehat{B_2}=45^0\)(\(\widehat{D_1}\)là góc ngoài\(\Delta ABD\)) ;\(\widehat{DBC}=75^0-15^0=60^0\)
\(\Delta BDC\)có\(\widehat{D_1}< \widehat{DBC}< \widehat{DCB}\left(45^0< 60^0< 75^0\right)\)nên BC < DC < BD
13 tháng 1 2018
vẽ tam giác EBC vuông cân tại E trong tam giác ABC
\(\widehat{EBC}=45^o\)
Ta có : EB2 + EC2 = BC2
2EB2 = 4 ; EB2 = 2 ; EB = \(\sqrt{2}\)
\(\Rightarrow\)EB = AD = \(\sqrt{2}\)
\(\Delta BAE\)= \(\Delta CAE\)( c.g.c ) suy ra : \(\widehat{BAE}=\widehat{CAE}=15^o\)
\(\widehat{ABC}=\left(180^o-30^o\right):2=75^o\)
\(\widehat{ABE}=75^o-45^o=30^o\)
\(\Rightarrow\)\(\widehat{ABE}=\widehat{BAD}=30^o\)
\(\Delta ABD=\Delta BAE\)( c.g.c ) suy ra : \(\widehat{ABD}=\widehat{BAE}=15^o\)
b) xét : \(\Delta DBC\)có : \(\widehat{DBC}=75^o-15^o=60^o\); \(\widehat{DCB}=75^o\)và \(\widehat{BDC}=45^o\)
suy ra : \(\widehat{BDC}< \widehat{DBC}< \widehat{DCB}\left(45^o< 60^o< 75^o\right)\)
Do đó : BC < CD < BD
YN
5 tháng 1 2022
Answer:
Tam giác ABC cân tại A mà góc BAC = 30 độ
=> Góc ABC = góc ACB = \(\frac{180^o-30^o}{2}=75^o\)
Kẻ AF vuông góc BC tại F; AE vuông góc BD tại E
Tam giác ABC cân tại A; góc A = 30 độ
=> Góc ABC = góc ACB = \(\frac{180^o-30^o}{2}=75^o\)
=> Góc ABE = góc ABC - góc DBC
=> Góc ABE = 75 độ - 60 độ = 15 độ
Ta xét tam giác ABE và tam giác BAF
Góc BAF = góc AEB
Góc AFB = góc AEB
AB là cạnh chung
=> Tam giác ABE = tam giác BAF (c.g.c)
\(\Rightarrow AE=BF=\frac{1}{2}BC=1cm\)
Tam giác BDC có: Góc DBC = 60 độ; góc BCD = 75 độ => Góc BDC = 45 độ
=> Góc BDC = góc ADE mà tam giác ADE vuông tại E
=> Tam giác ADE vuông cân tại E
=> AE = DE = 1cm
Tam giác AED vuông tại E \(\Rightarrow AD^2=AE^2+ED^2=1^2+1^2=2\)
\(\Rightarrow DA=\sqrt{2}\)
TM
21 tháng 2 2018
Tam giác ABC cân tại A, có góc A bằng 30 độ, suy ra góc B và C đều bằng 75 độ
vẽ hình ra nhé, kéo dài BD
từ A hạ đường vuông góc với BD cắt BD tại E
từ A cũng hạ đường vuông góc với BC cắt BC tại F
do góc BDC = 60 độ (đề bài cho)
nên góc ABE bằng 75-60=15 độ
xét 2 tam giác ABE và ABF
- AB chung
- góc BAF = góc ABE = 15 độ
- góc AFB = góc AEB = 90 độ
suy ra 2 tam giác bằng nhau (góc - cạnh - góc)
suy ra AE = BF = 1/2 BC = 1cm
xét tam giác nhỏ ADF ta có
- tam giác này vuông tại F
- góc DAF = 45 độ
suy ra tam giác này vuông cân tại F
suy ra AD = căn 2 AF = căn 2 cm
giải thích thêm chỗ góc DAF = 45 độ
do hai tam giác lớn cm bên trên bằng nhau suy ra góc BAF = góc ABE = 75 độ
góc BAC = 30 độ (đề bài cho)
suy ra góc DAF = 45 độ
P/s: chưa chắc đúng nha
Chúc các bn hok tốt !