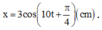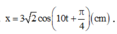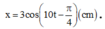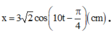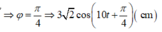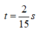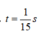1. tính độ cứng K và chiều dài tự nhiên của lò xo ?
2. Nếu gắn vào đầu dưới của lò xo vật có khối lượng m=250g . Tại vị trí cân bằng truyền cho vật vận tốc 40cm/s theo chiều (+) của trục toạ độ . Viết phương trình dao động
3. Tính lực đàn hồi và lực hồi phục ( của hệ cllx ở câu 2) khi vật ở vị trí cân bằng ? 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
Cách 1: Giải truyền thống
Biên độ dao động: A = x 2 + v 2 ω 2 = x 2 + v 2 m k = 3 2 + 30 2 .1 100 = 3 2 c m
Khi t = 0 → x = 3 → A = 3 2 x = A 2 v < 0 ⇒ φ = π 4 ⇒ 3 2 cos 10 t + π 4 c m
Cách 2: Dùng máy tính cầm tay
Cơ sở lí thuyết: x = A cos ω t + φ → t = 0 x ¯ = A cos φ + i sin φ (Biểu diễn phức).
Mặt khác: t = 0 → x = A cos φ v = − A ω sin φ ⇒ x ¯ = A cos φ + i sin φ = x − v ω i .
Bước 1: Bấm S H I F T M o d e 4 (Cài chế độ rad).
Bước 2: M o d e 2 S H I F T M o d e ∨ 3 2 (Cài chế độ tính toán).
Nhập biểu thức 3 − − 30 10 i màn hình xuất hiện.
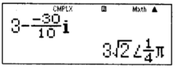
Chú ý: Do gốc tọa độ và chiều truyền vận tốc ta có x = 3 ; v < 0 . Các trường hợp khác thì dấu của x và v có thể thay đổi, bạn đọc cẩn thận chọn dấu cho phù hợp, tránh trường hợp chọn nhầm và nhập máy từ đó dẫn đến kết quả sai.

Đáp án A
+ Độ giãn của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 100 = 1 cm.
Tần số góc dao động của con lắc ω = k m = 10 10 rad/s.
+ Vận tốc truyền cho vật m so với điểm treo có độ lớn v 0 = 10 + 40 = 50 cm/s.
→ Biên độ dao động của vật sau đó A = v 0 ω = 50 10 10 = 1 , 58 cm.
→ Chiều dài cực đại l m a x = l 0 + Δ l 0 + A = 27 , 58 c m .

Chọn đáp án A
Δ l 0 = m g k = 2 , 5 c m ω = k m = 20 → A = x 2 + v 2 ω 2 A = l − Δ l 0 2 + v 2 ω 2 = 2 , 5 2 c m

Đáp án A
+ Ta tính được
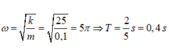
+ Độ biến dạng của lò xo khi vật ở vị trí cân bằng là
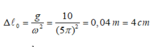
+ Từ VTCB, nâng vật lên 2 cm, tức là vật cách vị trí cân bằng 2 cm, suy ra |x| = 2 cm.
Áp dụng hệ thức liên hệ ta tính được biên độ dao động
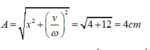
+ Sơ đồ chuyển động của vật được minh họa trên hình vẽ. Từ đó thay thấy thời điểm mà lúc vật qua vị trí lò xo dãn 6 cm lần hai (ở li độ x = 2 cm lần hai) là
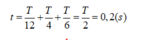

Đáp án C
Ta có ω 1 = ω 2 = ω 3 = 10 π rad / s
Phương trình dao động của vật 1 và vật 2 là:
x 1 = 3 cos ( 10 πt - π 2 ) c m x 2 = 1 , 5 cos ( 10 πt ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = ± A )
Trong quá trình dao động cả ba vật nằm trên một đường thẳng khi 2 x 2 = x 1 + x 3 ⇒ x 3 = 2 x 2 - x 1
tính chất trung bình
Bấm máy tính tổng hợp dao động ta được
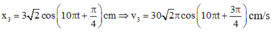
Taị t = 0 và v 30 = - 30 π cm / s
Trường hợp x 2 = 1 , 5 cos ( 10 π t + π ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = - A )
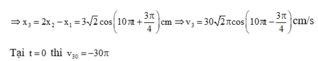

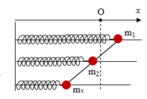
Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

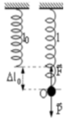
Tại VTCB ta có:
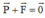 → P = F (1 điểm)
→ P = F (1 điểm)
→ mg = k (l – l 0 )
↔ 0,5.10 = 100(l - 0,5)
→ l = 0,55(m) = 55(cm) (1 điểm)