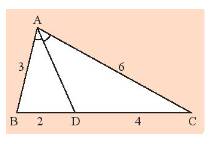
chứng minh đường phân giác góc ngoài của 1 góc trong 1 tam giác chia cạnh đối diện thành 2 đoạn thẳng tỉ lệ với 2 cạnh kề đoạn thẳng ấy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
Ta có: \(\frac{{BD}}{{DC}} = \frac{2}{4} = \frac{1}{2};\frac{{AB}}{{AC}} = \frac{3}{6} = \frac{1}{2}\).
Do đó, đường phân giác \(AD\) của tam giác đã chia cạnh \(BC\) thành hai đoạn là \(BD\) và \(DC\) tỉ lệ với hai cạnh \(AB\) và \(AC\).
29 tháng 8 2015
Dễ ẹt;
Giả sử \(\Delta\)ABC vuông tại A có phân giác AD sao cho DC=3BD;đương cao AH
Từ B kẻ đường thẳng song song với AC cắt AD tại I => BI vuông góc AB
Vì AD là p/g góc A => góc BAD=45 nên tam giác BAI vuông cân tại B nên BA=BI
Vì BI // AC nên \(\left(\frac{BI}{AC}\right)=\left(\frac{BD}{DC}\right)=\left(\frac{BD}{3BD}\right)=\frac{1}{3}\) (định lí Ta lét)
mà BI=AB nên \(\frac{AB}{AC}=\frac{1}{3}\)
Cm \(\Delta\)AHC đồng dạng \(\Delta\)BHA(g.g) nên \(\frac{BH}{HA}=\frac{HA}{HC}=\frac{AB}{AC}=\frac{1}{3}\)
nên \(BH=\frac{1}{3}AH\);\(HC=3AH\)nên \(\frac{BH}{HC}=\frac{1}{9}\)
6 tháng 9
Giả sử
Δ
ΔABC vuông tại A có phân giác AD sao cho DC=3BD;đương cao AH
Từ B kẻ đường thẳng song song với AC cắt AD tại I => BI vuông góc AB
Vì AD là p/g góc A => góc BAD=45 nên tam giác BAI vuông cân tại B nên BA=BI
Vì BI // AC nên
(
B
I
A
C
)
=
(
B
D
D
C
)
=
(
B
D
3
B
D
)
=
1
3
(
AC
BI
)=(
DC
BD
)=(
3BD
BD
)=
3
1
(định lí Ta lét)
mà BI=AB nên
A
B
A
C
=
1
3
AC
AB
=
3
1
Cm
Δ
ΔAHC đồng dạng
Δ
ΔBHA(g.g) nên
B
H
H
A
=
H
A
H
C
=
A
B
A
C
=
1
3
HA
BH
=
HC
HA
=
AC
AB
=
3
1
nên
B
H
=
1
3
A
H
BH=
3
1
AH;
H
C
=
3
A
H
HC=3AHnên
B
H
H
C
=
1
9
HC
BH
=
9
1
làm ngắn gọn thôi
ko cần hình đâu
Tham khảo: