Cho đường tròn (O,R) và một đường thẳng d không có điểm chung với đường tròn . Trên d lấy một điểm M bất kì , qua M kẻ các đường tròn (A,B là các tiếp điểm) . Kẻ đường kính AOC, tiếp điểm của (O) tại C cắt AB tại E. Tìm GTNN của dây AB và diện tích tứ giác MAOB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ACMO có
\(\widehat{CAO}+\widehat{CMO}=90^0+90^0=180^0\)
=>ACMO là tứ giác nội tiếp
=>A,C,M,O cùng thuộc một đường tròn
b: Xét (O) có
CA,CM là các tiếp tuyến
Do đó: CA=CM và OC là phân giác của góc AOM
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
OC là phân giác của góc AOM
=>\(\widehat{AOM}=2\cdot\widehat{MOC}\)
Ta có: OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{AOM}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOC}+2\cdot\widehat{MOD}=180^0\)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
Xét ΔOCD vuông tại O có OM là đường cao
nên \(OM^2=MC\cdot MD\)
mà MC=CA và MD=DB
nên \(AC\cdot BD=OM=R^2\) không đổi
c: Gọi N là trung điểm của CD
Xét hình thang ACDB(AC//DB) có
O,N lần lượt là trung điểm của AB,CD
=>ON là đường trung bình của hình thang ABDC
=>ON//AC//BD
=>ON\(\perp\)AB
Vì ΔCOD vuông tại O có N là trung điểm của CD
nên N là tâm đường tròn ngoại tiếp ΔCOD
Xét (N) có
NO là bán kính
AB\(\perp\)NO tại O
Do đó: AB là tiếp tuyến của (N)
=>AB là tiếp tuyến của đường tròn ngoại tiếp ΔCOD

1: ΔOAB cân tại O
mà OI là trung tuyến
nên OI vuông góc AB
góc OIM=góc OCM=góc ODM=90 độ
=>O,I,M,D,C cùng thuộc đường tròn đường kính OM
góc DIM=góc MOD
góc CIM=góc COM
mà góc COM=góc DOM
nên góc DIM=góc CIM
=>IM là phân giác của góc CID

a: Xét tứ giác OBMA có \(\widehat{OBM}+\widehat{OAM}=90^0+90^0=180^0\)
nên OBMA là tứ giác nội tiếp
=>O,B,M,A cùng thuộc một đường tròn
b: Ta có: ΔOBC cân tại O
mà OM là đường cao
nên OM là phân giác của góc BOC
Xét ΔOBM và ΔOCM có
OB=OC
\(\widehat{BOM}=\widehat{COM}\)
OM chung
Do đó: ΔOBM=ΔOCM
=>\(\widehat{OBM}=\widehat{OCM}\)
mà \(\widehat{OBM}=90^0\)
nên \(\widehat{OCM}=90^0\)
=>MC là tiếp tuyến của (O)
 a) Gọi D là trung điểm của MO
a) Gọi D là trung điểm của MO
∆OAM vuông tại A có AD là đường trung tuyến ứng với cạnh huyền OM
⇒ AD = OD = MD = OM : 2 (1)
∆OBM vuông tại B có BD là đường trung tuyến ứng với cạnh huyền OM
⇒ BD = OD = MD = OM : 2 (2)
Từ (1) và (2) ⇒ AD = BD = OD = MD
Vậy A, B, O, M cùng thuộc (D, AD)
b) Xét hai tam giác vuông: ∆OHB và ∆OHC có:
OH là cạnh chung
OB = OC = bán kính
⇒ ∆OHB = ∆OHC (cạnh huyền - cạnh góc vuông)
⇒ ∠HOB = ∠HOC (hai góc tương ứng)
⇒ ∠MOB = ∠MOC
Xét ∆MOB và ∆MOC có:
OM là cạnh chung
∠MOB = ∠MOC (cmt)
OB = OC = bán kính)
⇒ ∆MOB = ∆MOC (c-g-c)
⇒ ∠OBM = ∠OCM (hai góc tương ứng)
⇒ ∠OCM = 90⁰
⇒ MC ⊥ OC
Mà OC là bán kính của (O)
⇒ MC là tiếp tuyến của (O)

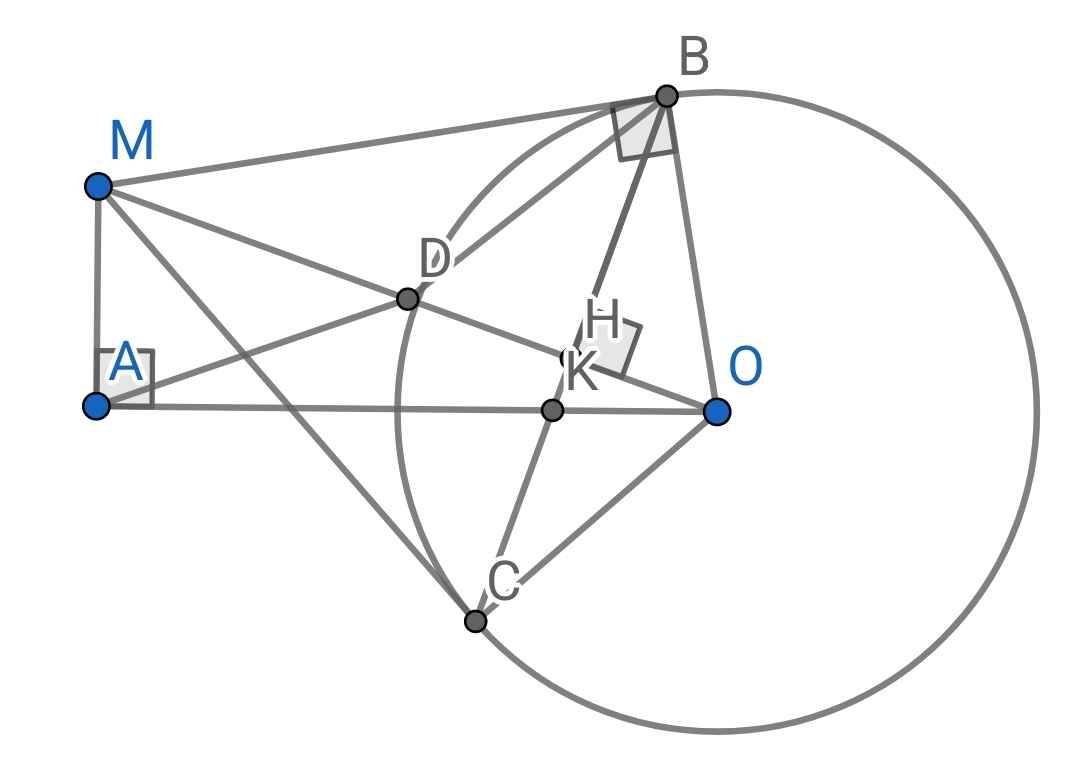
a: góc MHO=góc MBO=góc MAO=90 độ
=>M,A,O,B,H nội tiếp
b: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại I
Xét ΔOIK vuông tại I và ΔOHM vuông tại H có
góc IOK chung
=>ΔOIK đồng dạng với ΔOHM
=>OI/OH=OK/OM
=>OI*OM=OH*OK