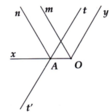
Cho x O y ^ = 120 ° . Lấy điêm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho O A t ^ = 60 ° .a) Chứng minh At // Oy.b) Gọi On, Om lần lượt là 2 tia phân giác của x...

TT

Trần Trung Quân

27 tháng 9 2021

Cho x O y ^ = 120 ° . Lấy điêm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho O A t ^ = 60 ° .a) Chứng minh At // Oy.b) Gọi On, Om lần lượt là 2 tia phân giác của x O y ^ và x A t ^. Chứng minh On // Am Giúp mk...

Đọc tiếp

#Toán lớp 7

0

PT

Pham Trong Bach

29 tháng 8 2017

Cho x O y ^ = 120 ° . Lấy điêm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho O A t ^ = 60 ° . Gọi At' là tia đối của tia At.

a) Chứng minh tt' // Oy.

b) Gọi Om và An theo thứ tự là các tia phân giác của các góc xOy và xAt. Chứng minh Om // An

#Toán lớp 7

1

CM

Cao Minh Tâm

29 tháng 8 2017

Đúng(0)

MT

Minh Thắng Trịnh

20 tháng 7 2021

cũng hay,cũng được

Đúng(0)

PT

Pham Trong Bach

21 tháng 3 2017

Cho x O y ^ = 120 ° . Lấy A trên tia Ox. Trên cùng một nửa mặt phẳng bờ Ox có chứa Oy, vẽ tia At sao cho O A t ^ = 60 ° a. Chứng tỏ At // Oyb) Gọi On và Am lần lượt là hai tia phân giác của x O y ^ và x A t ^ . Chứng tỏ On //...

Đọc tiếp

#Toán lớp 7

1

CM

Cao Minh Tâm

21 tháng 3 2017

a. Ta có t A O ^ + A O y ^ = 120 ° + 60 ° = 180 ° mà 2 góc này ở vị trí kề bù nên At // Oy

b. Ta có được A ^ 1 = A 2 ^ = 1 2 A ^ ( tính chất tia phân giác); O ^ 1 = O ^ 2 = 1 2 O ^ (tính chất tia phân giác)

Mặt khác x A t ^ = A O y ^ (cmt) ⇒ A ^ 2 = O ^ 2 mà 2 góc ấy ở vị trí đồng vị => hai đường phân giác song song với nhau

Đúng(0)

HW

Hibiki Watanabe

29 tháng 7 2017 - olm

Cho xOy = 120 độ, lấy điểm A thuộc Ox trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho OAt = 60 độ. Gọi At' là tia đối của At.

a) Chứng tỏ tt' // Oy

b) Gọi Om, An lần lượt là tia phân giác của xOy, xAt. Chứng tỏ Om // An.

#Toán lớp 7

1

CG

Cu Giai

29 tháng 7 2017

a/) có góc xoy = 120 độ

góc oat = 60 độ

=> 2 góc đó + vs nhau = 180 độ ( viết hẳn góc ra)

mà 2 góc đó ở vị trí trong cùng phía

=> oy//tt'

b)

Đúng(0)

AL

áo lớp đẹp

12 tháng 6 2018 - olm

Cho xOy = 120 độ, lấy điểm A thuộc Ox trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho OAt = 60 độ. Gọi At' là tia đối của At.

a) Chứng tỏ tt' // Oy

b) Gọi Om, An lần lượt là tia phân giác của xOy, xAt. Chứng tỏ Om // An.

#Toán lớp 7

0

PT

Pham Trong Bach

30 tháng 12 2018

Cho x O y ^ = 120°. Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho O A t ^ = 60°. Gọi At' là tia đối của tia At.a) Chứng minh tt' // Oy.b) Gọi Om và An theo thứ tự là các tia phân giác của các góc xOy và xAt. Chứng minh Om //...

Đọc tiếp

#Toán lớp 7

1

CM

Cao Minh Tâm

30 tháng 12 2018

a) O A t ^ + x O y ^ = 60°+ 120° = 180° (hai góc trong cùng phía bù nhau)

=> At // Oy => tt' // Oy

b) Vì Om là phân giác x O y ^ nên:

x O m ^ = 1 2 x O y ^ = 1 2 .120° = 60° (1)

Mặt khác : O A t ^ = 60 ° = > x A t ^ = 120°

Vì An là phân giác x A t ^ nên:

x A n ^ = 1 2 x A t ^ = 1 2 .120° = 60° (2)

Từ (1) và (2) suy ra x O m ^ = x A n ^ .

Do đó Om // An

Đúng(0)

MK

Mi Ka

9 tháng 10 2021

góc xOy=120 độ , lấy điểm A trên tia Ox . trên cùng nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho góc OAt=60 độ . gọi At` là tia đối của tia Ata, chứng minh rằng : tt` // Oyb, gọi Om // An là phân giác của góc xOy và góc OAtchứng minh rằng : Om // An ...

Đọc tiếp

#Toán lớp 7

0

S

sakuraharuno1234

6 tháng 10 2021

Cho xOy=120 độ. Lấy điểm A trên tia Ox. Trên cùng một nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho OAt= 60 độ. Gọi A't là tia đối tia At

A)Chứng mính tt' // Oy

B)Gọi Om và An theo thứ tự là các tia phân giác của góc xOy và xAt.Chứng minh Om//An

Vẽ hình và giải không được tắt nha mọi người

#Toán lớp 7

0

S

sakuraharuno1234

6 tháng 10 2021

Cho xOy=120 độ. Lấy điểm A trên tia Ox. Trên cùng một nửa mặt phẳng bờ Ox chứa tia Oy vẽ tia At sao cho OAt= 60 độ. Gọi A't là tia đối tia At

A)Chứng mính tt' // Oy

B)Gọi Om và An theo thứ tự là các tia phân giác của góc xOy và xAt.Chứng minh Om//An

Vẽ hình giúp mình nha

#Toán lớp 7

0

TA

Tiếng anh123456

8 tháng 10 2023

Cho góc xOy = 120°. Lấy điểm A trên tia Ox. Trên cùng nửa mặt phẳng chứa tia Oy bờ là tia Ox, vẽ tia At sao cho góc OAt = 60°. Gọi At' là tia đối của tia At. a) Chứng minh tt' // Oy. b) Gọi Om và An theo thứ tự là các tia phân giác của các góc xOy và xAt. Chứng minh Om //...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

8 tháng 10 2023

a: \(\widehat{tAO}+\widehat{xOy}=180^0\)

mà hai góc này trong cùng phía

nên tt'//Oy

b: \(\widehat{xAt}+\widehat{tAO}=180^0\)

=>\(\widehat{xAt}=180^0-60^0=120^0\)

=>\(\widehat{xAn}=\dfrac{120^0}{2}=60^0\)

Om là phân giác của góc xOy

=>\(\widehat{xOm}=\dfrac{1}{2}\cdot120^0=60^0\)

\(\widehat{xOm}=\widehat{xAn}\)

mà hai góc này ở vị trí đồng vị

nên Om//An

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP