Bài 6: Giao điểm hai đường chéo của hình vuông gọi là “tâm” của hình vuông
đó. Hãy tìm cách cắt mảnh giấy hình vuông rồi xếp lại thành một chiếc “chong
chóng 4 cánh”, đục thủng tâm, gắn trục để chong chóng quay khi có gió.
giải giúp ekm ợ!plz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 9 2018
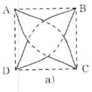
a) Cách vẽ:
- Vẽ hình vuông ABCD.
- Vẽ cung tròn tâm A, bán kính là cạnh hình vuông. Cung tròn này đi qua B, D.
- Tương tự với các cung tròn còn lại.
Ta được bốn cung tròn tạo thành hình hoa bốn cánh.
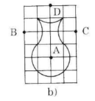
b) Cách vẽ:
- Kẻ lại các ô vuông và lấy các điểm như hình 61.
- Lần lượt vẽ các cung tròn có tâm là các điểm A, B, C, D, E và bán kính là đường chéo của ô vuông.
Ta được năm cung tròn liền nét với nhau tạo thành hình chiếc lọ hoa.
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
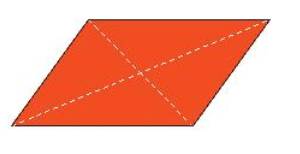
Giao điểm của hai đường chéo là tâm đối xứng của hình bình hành vì khi quay hình bình hành một nửa vòng quanh điểm đó thì thu được hình chồng khít với hình bình hành ban đầu.
CM
22 tháng 4 2017
Đáp án: B
a sai vì trực tâm là giao điểm của ba đường cao, không phải ba đường phân giác.
b sai vì hai đường chéo của hình bình hành không bằng nhau.
c, d, e đúng.
CM
8 tháng 1 2018
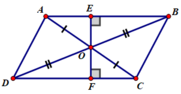
- Hình bình hành ABCD có O là giao điểm của hai đường chéo ⇒ O là trung điểm mỗi đường nên A và C đối xứng nhau qua tâm O
B và D đối xứng nhau qua tâm O
- Xét hai tam giác vuông AEO và CFO có:
OA = OC (do O là trung điểm AC)
∠(AOE) = ∠(COF)(hai góc đối đỉnh)
⇒ ΔAEO = ΔCFO (cạnh huyền – góc nhọn kề)
⇒ OE = OF (hai cạnh tương ứng)
Nên O là trung điểm EF
⇒ E và F đối xứng nhau qua tâm O