Một xilanh nằm ngang .một pittông cách nhiệt, lúc đầu cách đều hai đầu xilanh khoảng 50cm và không khí chứa trong hai phần xi lanh ở 27 độ C ,áp suất 1at sau đó chất khí ở phần bên trái nung thêm 20 đ...

TV

Trung's Việt'j Trần's

23 tháng 12 2018

Một xilanh nằm ngang .một pittông cách nhiệt, lúc đầu cách đều hai đầu xilanh khoảng 50cm và không khí chứa trong hai phần xi lanh ở 27 độ C ,áp suất 1at sau đó chất khí ở phần bên trái nung thêm 20 độ C .bên phải giảm 20 độ C thì p dịch chuyển khoản x. hỏi pitong dịch chuyển về phía nào. tính X và áp suất trong...

Đọc tiếp

#Vật lý lớp 10

1

TD

Thần đồng toán

26 tháng 10

P1=47,P2=53

(P1V1)/T1=(P2V2)/T2

=>T2=65,3°C

Đúng(0)

ML

Mai Lê

23 tháng 4 2021

Một xylanh đươc nằm ngang, lúc đầu piston cách nhiệt và cách đều 2 đầu xylanh 1 khoảng l = 50cm và không khí chứa trong xylanh có nhiệt độ 27°C áp suất 1atm. Sau đó không khí ở đầu bên trái được nung nóng lên 67°C thì piston sẽ di chuyển 1 đoạn x, tìm giá trị của x.

#Vật lý lớp 10

0

BT

Bé Thương

17 tháng 3 2016

Một xilanh đặt nằm ngang, hai đầu kín, có thể tích 2V0 và chứa khí lí tưởng ở áp suất p0. Khí trong xilanh được chia thành hai phần bằng nhau nhờ một pit-tông mỏng, cách nhiệt có khối lượng m. Chiều dài của xilanh là 2l. Ban đầu khí trong xilanh có nhiệt độ là T0, pit-tông có thể chuyển động không ma sát dọc theo xi lanh.a Nung nóng chậm một phần khí trong xilanh để nhiệt độ tăng thêm...

Đọc tiếp

#Vật lý lớp 10

1

LU

lưu uyên

17 tháng 3 2016

a) Phần xi lanh bi nung nóng: \(\frac{P_oV_o}{T_o}=\frac{P_1V_1}{T_1}=\frac{P_1V_1}{T_0+\Delta T}\)

Phần xi lanh bị làm lạnh: \(\frac{P_oV_o}{T_o}=\frac{P_2V_2}{T_2}=\frac{P_2V_2}{T_0-\Delta T}\)

Vì P₁ = P₂ \(\rightarrow\frac{V_1}{V_2}=\frac{T_0+\Delta T}{T_0-\Delta T}\) (1)

Gọi đoạn di chuyển của pit-tông là x, ta có: V₁ = (l + x)S và V₂ = (l - x)S (2)

Từ (1) và (2) ta có \(\frac{\left(l+x\right)S}{\left(l-x\right)S}=\frac{T_0+\Delta T}{T_0-\Delta T}\rightarrow\) x = \(\frac{l\Delta T}{T_0}\)

b) P₂V₂ = P₀V \(\rightarrow\) P₂ = P₀V₀ /(l - x)S (1)

P₁V₁ = P₀V \(\rightarrow\) P₂ = P₀V₀/(l + x)S (2)

Xét pit-tông: F₂ - F₁ = ma \(\rightarrow\) (P₂ - P₁)S = ma (3)

Từ (1), (2), và (3)

\(\left(\frac{P_0V}{S\left(l-r\right)}\right)-\left(\frac{P_0V}{S\left(l+r\right)}\right)S\)= ma \(\rightarrow\) a = 2P₀V₀x/(l² – x²)m

Đúng(0)

HD

Hoàng Đức Long

9 tháng 12 2018

Một xilanh có pit-tông cách nhiệt đặt nằm ngang. Pit-tông ở vị trí chia xilanh thành hai phần bằng nhau, chiều dài của mỗi phần là 30 cm. Mỗi phần chứa một lượng khí như nhau ở nhiệt độ 17 ° C và áp suất 2 atm. Muốn pit-tông dịch chuyển 2 cm thì phải đun nóng khí ở một phần lên thêm bao nhiêu độ ? Áp suất của khí khi pit-tông đã dịch chuyển là bao nhiêu...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

9 tháng 12 2018

Đối với phần khí bị nung nóng:

+ Trạng thái đầu: p 1 ; V 1 = lS; T 1 (1)

+ Trạng thái cuối: p 2 ; V 2 = (l + ∆ l)S; T 2 (2)

Đối với phần khí không bị nung nóng:

+ Trạng thái đầu: p 1 ; V 1 = lS; T 1 (1)

+ Trạng thái cuối: p ' 2 ; V ' 2 = (l - ∆ l)S; T ' 2 = T 1 (2)

Ta có:

p 1 V 1 / T 1 = p 2 V 2 / T 2 = p ' 2 V ' 2 / T 1

Vì pit-tông ở trạng thái cân bằng nên p ' 2 = p 2 . Do đó

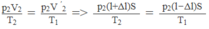
Giải sách bài tập Vật Lí 10 | Giải sbt Vật Lí 10

⇒ T 2 = (l + ∆ l/l - ∆ l). T 1

Vậy phải đun nóng khí ở một bên lên thêm ∆ T độ:

Vì p 1 V 1 / T 1 = p 2 V 2 / T 2 nên:

Thay số vào ta được:

p 2 ≈ 2,14(atm)

Đúng(0)

SK

Sakumorisa Kinoharu

28 tháng 4 2021

Một khối khí chứa trong một xi - lanh kín đặt nằm ngang ở áp suất 10 Pa có thể tích 7 lít và nhiệt độ ban đầu 25 ° C . Nung nóng khí trong xi - lanh , khí dãn nở đằng áp ở nhiệt độ 125 ° C . a . Tính thể tích khí sau khi nung nóng . b . Nếu trong quá tình nung nóng khi nhận được nhiệt lượng 700J . Tính độ biến thiên nội năng của khí .

#Vật lý lớp 10

0

4L

40.Việt Lê Văn

29 tháng 5 2022

Một khối khí trong xilanh lúc đầu có hai áp suất 2 atm nhiệt độ 27°c và thể tích 150 cm³ khi pittông nén khí đến 50 cm³ và áp suất 10 atm thì nhiệt độ cuối cùng của khối khí là bao nhiêu

#Vật lý lớp 10

1

VV

Viêm Vũ

29 tháng 5 2022

P1=2atm

T1=27+273=300k

V1=150cm3=0,15l

P2=10atm

V2=50cm3=0,05l

T2=? K

Giai

P1.V1/T1=P2.V2/T2

2.0,15/300=10.0,05/T2

=> T2= 500K

Đúng(2)

NT

Ngọc Tường Vi Nguyễn

8 tháng 11 2016

một khối khí trong xi lanh lúc đầu có áp suất 1at, nhiệt độ 57 C và thể tích là 150cm3. Khi pittông nén khí đến 30cm3 và áp suất là 10at thì nhiệt độ cuối cùng là?

#Vật lý lớp 10

1

DT

Dương Thị Thu Mai

10 tháng 5 2018

p1=1atm,t1=57°C=>T1=330K,V1=150cm^3=>1500l

p2=10atm,V2=30cm^3=>300l,t1=?=>T2=?

Giải:p1×V1/T1=p2×V2/T2=>T2=p2×V2×T1/p1×V1=10×300×330/1×1500=660K=>t2=660-273=387°C

Đúng(0)

HD

Hoàng Đức Long

15 tháng 10 2017

Đẩy pit-tông của một xilanh đủ chậm để nén lượng khí chứa trong xilanh sao cho thể tích của lượng khí này giảm đi 2 lần ở nhiệt độ không đổi. Khi đó áp suất của khí trong xi lanh

A. giảm đi 2 lần. B. tăng lên 2 lần.

C. tăng thêm 4 lần. D. không thay đổi.

#Vật lý lớp 10

1

VT

Vũ Thành Nam

15 tháng 10 2017

Chọn đáp án B

Đúng(0)

HE

hằng em

21 tháng 2 2022

một xilanh chứa 200 cm3 khí ở áp suất 3.105 Pa . Pit-tông nén khí xilanh xuống còn 100 cm3 . Tính áp suất của khí trong xilanh lúc sau , coi như nhiệt độ không...

Đọc tiếp

#Vật lý lớp 10

1

DT

Đỗ Tuệ Lâm

21 tháng 2 2022

cu ap dung cong thuc la ra, giai:

Xét lượng khí trong xi lanh.

Áp dụng định luật Bôilơ – Mariốt ta có:

\(p_1V_1=p_2V_2\Rightarrow p_2=\dfrac{p_1V_1}{V_2}=\dfrac{3.10^5.200}{100}=600000\left(Pa\right)\)

Đúng(2)

HD

Hoàng Đức Long

10 tháng 12 2018

Một xilanh chứa 150cm3 khí ở áp suất 2.105 Pa.Pit-tông nén khí trong xilanh xuống còn 100cm3.Tính áp suất của khí trong xilanh lúc này, coi nhiệt độ như không đổi.

#Vật lý lớp 10

1

VT

Vũ Thành Nam

10 tháng 12 2018

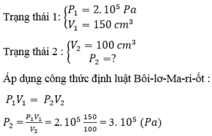
Giải bài tập Vật Lý 10 | Để học tốt Vật Lý 10

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP