Cho (O) đường kính AB=10cm C là 1 điểm trên đường tròn (O) sao cho AC=6cm Vẽ CH vuông góc với AB (H thuộc AB)
a) Tính AH và góc ABC
b) Tiếp tuyến tại B và C của (O) cắt nhau tại D chứng minh rằng OD vuông góc với BC
c) Tiếp tuyến tại A của (O) cắt BC tại E chứng minh CE.CB=AH.AB
d) Gọi I là trung điểm của CH tia BI cắt AE tại F chứng minh FC là tiếp tuyến của...
Đọc tiếp
Cho (O) đường kính AB=10cm C là 1 điểm trên đường tròn (O) sao cho AC=6cm Vẽ CH vuông góc với AB (H thuộc AB)
a) Tính AH và góc ABC
b) Tiếp tuyến tại B và C của (O) cắt nhau tại D chứng minh rằng OD vuông góc với BC
c) Tiếp tuyến tại A của (O) cắt BC tại E chứng minh CE.CB=AH.AB
d) Gọi I là trung điểm của CH tia BI cắt AE tại F chứng minh FC là tiếp tuyến của (O)
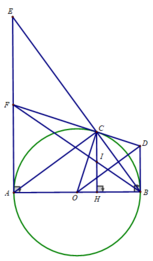
a) Có \(\Delta ABC\) vuông tại C (AB là đường kính)
Theo htl, ta có: \(AH=\dfrac{AC^2}{AB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Có: \(sinB=\dfrac{AC}{AB}=\dfrac{6}{10}=\dfrac{3}{5}\Rightarrow\widehat{B}\approx37^O\)
b) Có: \(\Delta_vOCD=\Delta_vOBD\left(ch-cgv\right)\)
\(\Rightarrow\widehat{COD}=\widehat{BOD}\)
mà \(\Delta BOC\) cân tại O(OB=OC=R)
\(\Rightarrow\)OD là đường phân giác đồng thời là đường cao.
\(\Rightarrow OD\perp BC.\)
c)Theo htl cho \(\Delta_VEAB\):
\(AC^2=CE.CB\)
Theo htl cho \(\Delta_VABC\):
\(AC^2=AH.AB\)
\(\Rightarrow CE.CB=AH.AB.\)