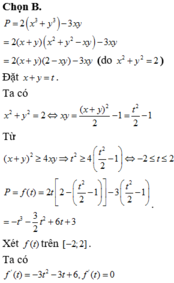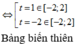Cho x và y là hai số thực thỏa mãn x2 + y2 = 1. Hãy tìm giá trị lớn nhất của biểu thức M = x5 + 2y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 12 2019
Đáp án D
Phương pháp giải:
Đặt ẩn phụ, đưa về hàm một biến, dựa vào giả thiết để tìm điều kiện của biến
Lời giải:
Từ giả thiết chia cả 2 vế cho x2y2 ta được :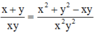 
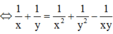
Đặt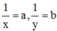 
ta có 
Khi đó 
Ta có 
mà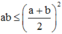 
nên 
Dấu đẳng thức xảy ra khi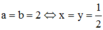 
. Vậy Mmax = 16
CM
9 tháng 1 2018
Đáp án B
Ta có P = 2 x 3 + y 3 - 3 x y = 2 x + y x 2 - x y + y 2 - 3 x y = 2 x + y 2 - x y - 3 x y
Mặt khác x 2 + y 2 = 2 ⇔ x + y 2 - 2 x y = 2 ⇔ 2 x y = x + y 2 - 2 ≤ x + y 2 2 ⇔ - 2 ≤ x + y ≤ 2
Khi đó 2 P = 2 x + y 4 - 2 x y - 6 x y = 2 x + y 4 - x + y 2 + 2 - 3 x + y 2 - 2
= 6 + 12 x + y - 3 x + y 2 - 2 x + y 3 = f t = 6 + 12 t - 3 t 2 - 2 t 3
Với t = x + y ∈ - 2 ; 2
Xét hàm số f t = 6 + 12 t - 3 t 2 - 2 t 3 trên đoạn [-2;2] ta có
f ' t = 12 - 6 t - 6 t 2 ; f ' t = 0 ⇔ [ t = - 2 t = 1
So sánh các giá trị f(-2);f(1);f(2), ta được m a x - 2 ; 2 f t = f 1 = 13 ⇒ M = 13 2 .
KN
31 tháng 1 2020
Bạn tham khảo nhé!
Câu hỏi của Lê VĂn Chượng - Toán lớp 10 - Học toán với OnlineMath
CM
6 tháng 11 2017
Chọn B.
P =
2
(
x
3
+
y
3
)
-
3
x
y
(do
x
2
+
y
2
=
2
)
Đặt x + y = t. Ta có
x
2
+
y
2
=
2
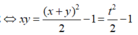
Từ 
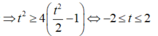
P = f(t)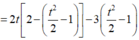 
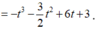
Xét f(t) trên [-2;2].
Ta có 
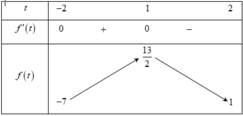
Bảng biến thiên
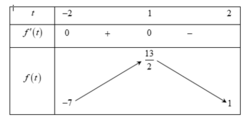
Từ bảng biến thiên ta có max P = max f(t) = 13 2 ; min P = min f(t) = -7
Lời bình: Có thể thay bbt thay bằng
Ta có 
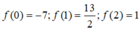
Suy ra kết luận.
CM
22 tháng 9 2019
Áp dụng bất đẳng thức Cosi ta có:
1 32 32 x 29 x + 3 y ≤ 1 4 2 32 x + 29 x + 3 y 2 = 1 8 2 61 x + 3 y
Tương tự
1 32 32 y 29 y + 3 x ≤ 1 8 2 61 y + 3 x
=> P ≤ 4 2 x + y ≤ 4 2 x 2 + 1 2 + y 2 + 1 2 = 8 2
Vậy P min = 8 2 <=> x = y = 1