Cho tam giác ABC. Vẽ đường tròn tâm B bán kính AC, đường tròn tâm C bán kính AB. Hai đường tròn này cắt nhau tại hai điểm E và F thuộc hai nửa mặt phẳng đối nhau bờ là đường thẳng BC. CMR: AE//BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 2 2021
a) Xét (O) có
ΔBDC nội tiếp đường tròn(B,D,C∈(O))
BC là đường kính(gt)
Do đó: ΔBDC vuông tại D(Định lí)
⇔CD⊥BD tại D
⇔CD⊥AB tại D
⇔\(\widehat{ADC}=90^0\)
hay \(\widehat{ADH}=90^0\)
Xét (O) có
ΔBEC nội tiếp đường tròn(B,E,C∈(O))
BC là đường kính(gt)
Do đó: ΔBEC vuông tại E(Định lí)
⇔BE⊥CE tại E
⇔BE⊥AC tại E
⇔\(\widehat{AEB}=90^0\)
hay \(\widehat{AEH}=90^0\)
Xét tứ giác ADHE có
\(\widehat{ADH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{ADH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét ΔABE vuông tại E và ΔACD vuông tại D có
\(\widehat{BAE}\) chung
Do đó: ΔABE∼ΔACD(g-g)
⇔\(\dfrac{AB}{AC}=\dfrac{AE}{AD}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB\cdot AD=AC\cdot AE\)(đpcm)
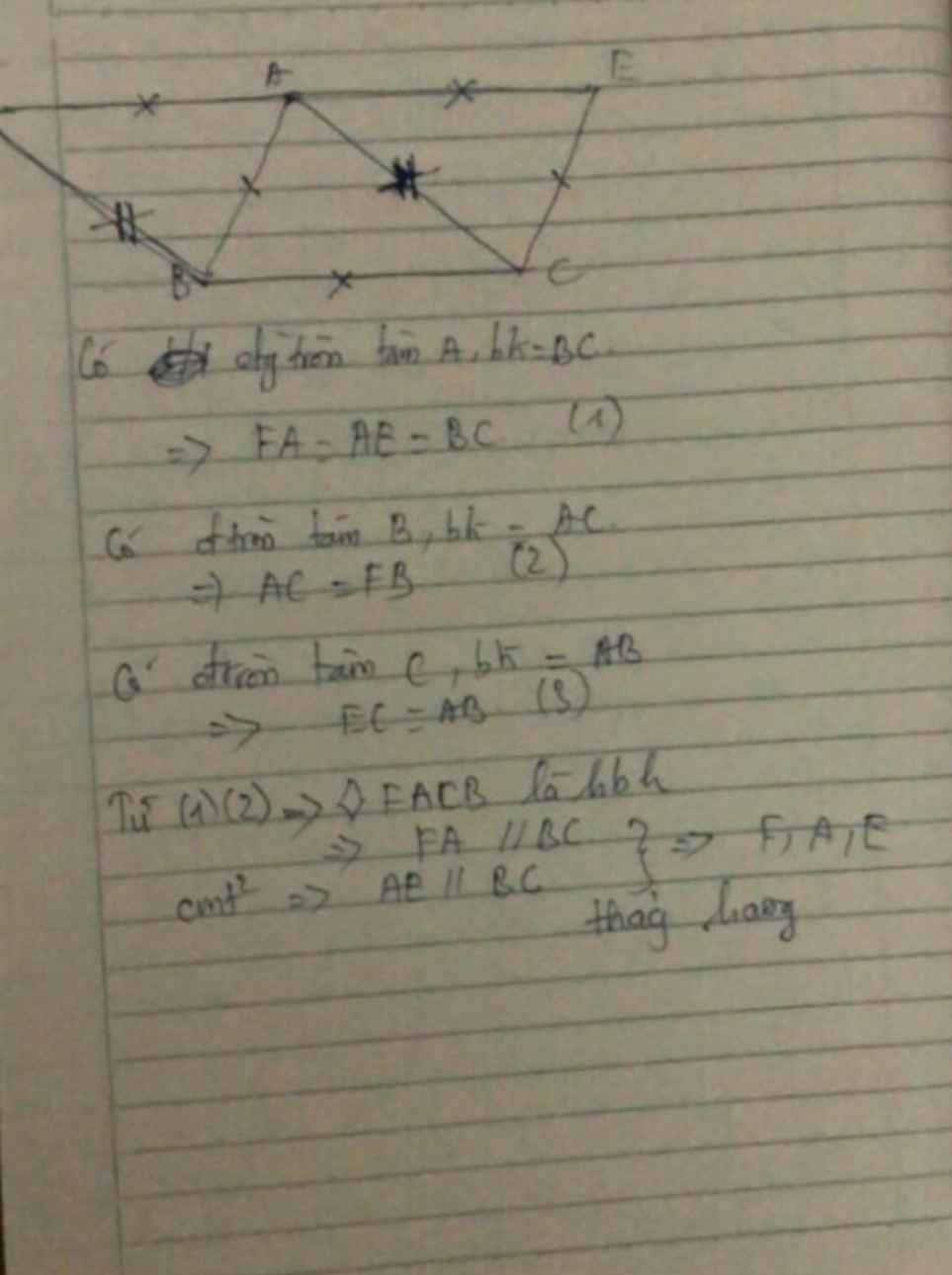
Xét tứ giác ABFC có
AB=FC
AC=BF
Do đó; ABFC là hình bình hành
=>CF//AB và CF=AB
Xét ΔABC và ΔECB co
AB=EC
BC chung
AC=BE
Do đo: ΔABC=ΔECB
=>góc ABC=góc ECB
Gọi giao của AB và EC là G
Xét ΔGBC có góc GBC=góc GCB
nên ΔGBC cân tại G
=>GB=GC
=>GA=GE
Xét ΔGBC có GA/GB=GE/GC
nên AE//BC