Cho tam giác ABC , M là trung điểm của BC, G là trọng tâm tam giác ABC . Lấy D đối xứng với A qua M , I là trọng tâm của tam giác MCD .
Chứng minh \(\overrightarrow{IG}=\dfrac{1}{3}\overrightarrow{AB}+\overrightarrow{DM}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

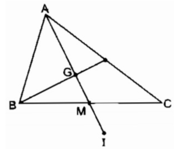
I đối xứng với A qua tâm G
ta có: GA = GI, GM ∈ GA ( tính chất đường trung tuyến của tam giác)
Suy ra: GM ∈ GI
Mà: GM + MI = GI và GM = AG/2 (tính chất đường trung tuyến) =>GM = GI/2
Suy ra: GM = MI nên điểm M là trung điểm của GI
Vậy I đối xứng với G qua M.