Cho đường tròn tâm O bán kính R và đường thẳng (\(\Delta\)) không có điểm chung với đường tròn (O) , H là hình chiếu vuông góc của O trên (\(\Delta\)) . Từ điểm M bất kỳ trên (\(\Delta\)) (M\(\ne\)H) , vẽ hai tiếp tuyến MA, MB tới đường tròn (O) (A,B là hai tiếp điểm ) . Gọi K, I thứa tự là giao điểm của AB với OM và OH .
1. chứng minh AB=2AK và 5 điểm M;A;O;B;H cùng thuộc đường tròn .
2. Chứng minh...
Đọc tiếp
Cho đường tròn tâm O bán kính R và đường thẳng (\(\Delta\)) không có điểm chung với đường tròn (O) , H là hình chiếu vuông góc của O trên (\(\Delta\)) . Từ điểm M bất kỳ trên (\(\Delta\)) (M\(\ne\)H) , vẽ hai tiếp tuyến MA, MB tới đường tròn (O) (A,B là hai tiếp điểm ) . Gọi K, I thứa tự là giao điểm của AB với OM và OH .
1. chứng minh AB=2AK và 5 điểm M;A;O;B;H cùng thuộc đường tròn .
2. Chứng minh OI.OH=OK.OM=R\(^2\)
3. Trên đoạn OA lấy điểm N sao cho AN=2ON. Đường trung trực của BN cắt OM ở E . Tính tỷ số \(\dfrac{OE}{OM}\)
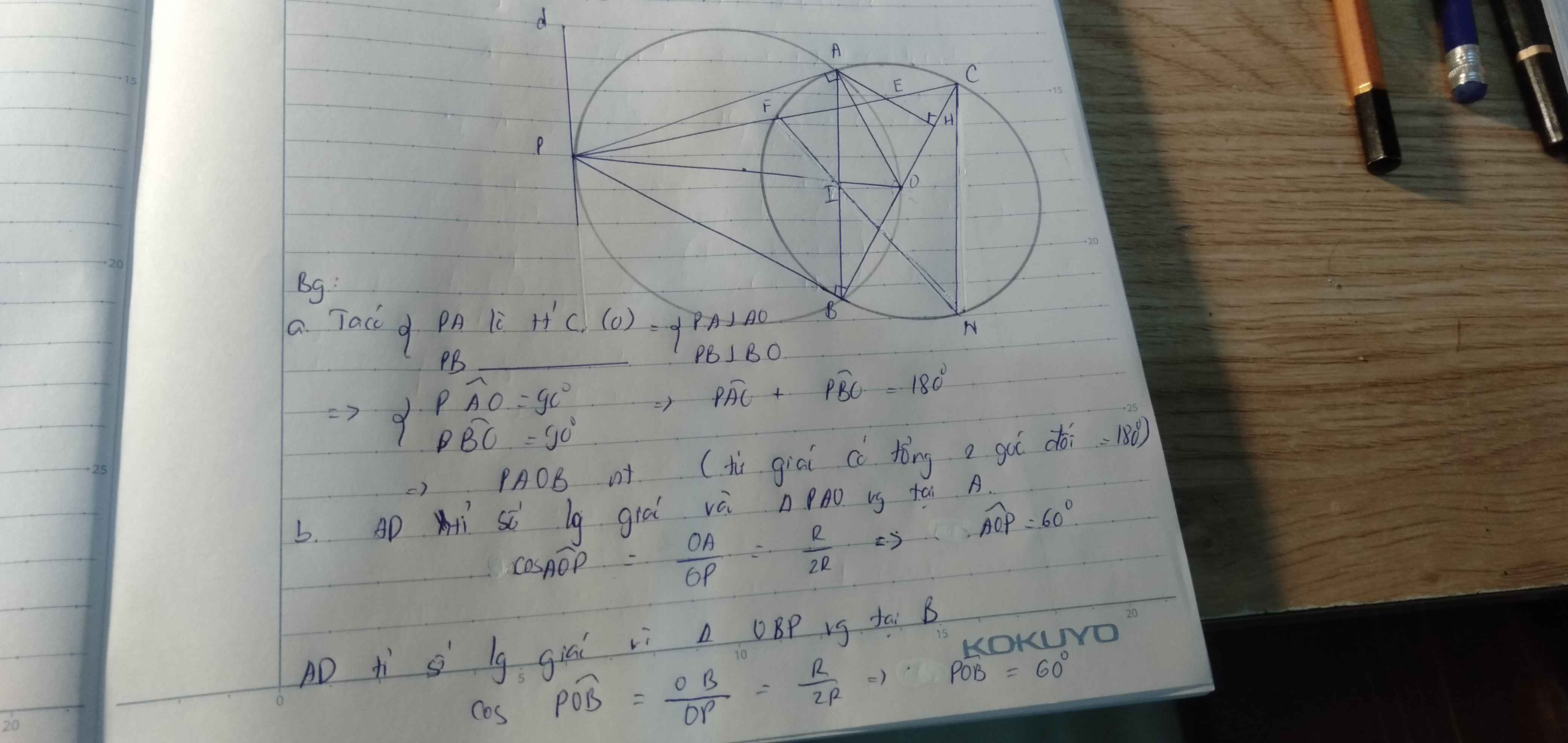
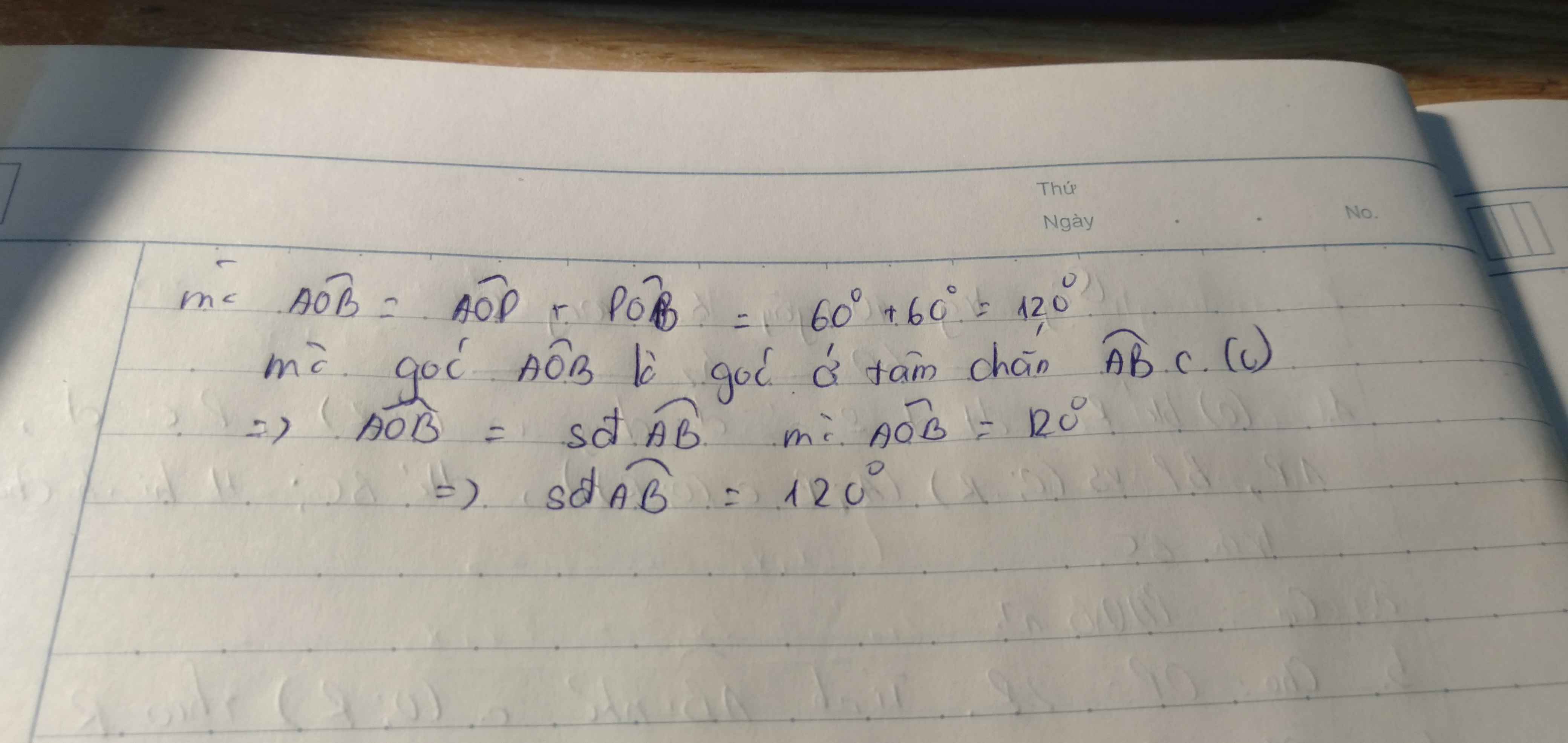
1: Xét (O) có
MA,MB là các tiếp tuyến
nên MA=MB
mà OA=OB
nên OM là đường trung trực của AB
=>OM vuông góc với AB
Ta có: ΔOAB cân tại O
mà OK là đường cao
nên K là trug điểm của BA
=>AB=2AK
Xét tứ giác OAMB có góc OAM+góc OBM=180 độ
nên OAMB là tứ giác nội tiếp(1)
Xét tứ giác OAMH có góc OAM+góc OHM=180 độ
nên OAMH là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra O,A,M,B,H cùng thuộc 1 đường tròn
2: Xét ΔOBI và ΔOHB có
góc OBI=góc OHB
góc IOB chung
DO đó: ΔOBI đồng dạng với ΔOHB
=>OB/OH=OI/OB
=>OI*OH=OB^2=R^2
Xét ΔOAM vuông tại A có AK là đường cao
nên OK*OM=OA^2=R^2