Giải phương trình: \(\dfrac{1}{x^2+4x+3}+\dfrac{1}{x^2+8x+15}+\dfrac{1}{x^2+12x+35}+\dfrac{1}{x^2+16x+63}=\dfrac{1}{5}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) \(\left(x-3\right)^2+3x-22=\sqrt{x^2-3x+7}\)
\(\Leftrightarrow x^2-6x+9+3x-22=\sqrt{x^2-3x+7}\)
\(\Leftrightarrow\left(x^2-3x+7\right)-\sqrt{x^2-3x+7}-20=0\)
Đặt \(\sqrt{x^2-3x+7}=t\left(t\ge0\right)\left(1\right)\)
\(\Rightarrow t^2-t-20=0\)
\(\Rightarrow x_1=5\left(TM\right);x_2=-4\left(KTM\right)\)
Thay t=5 vào (1), ta có :
\(\sqrt{x^2-3x+7}=5\)
\(\Leftrightarrow x^2-3x+7=25\)
\(\Leftrightarrow x^2-3x-18=0\)
\(\Rightarrow x_1=6;x_2=-3\)
vậy...

1.
\(x^4-6x^2-12x-8=0\)
\(\Leftrightarrow x^4-2x^2+1-4x^2-12x-9=0\)
\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=2x+3\\x^2-1=-2x-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\\x^2+2x+2=0\end{matrix}\right.\)
\(\Leftrightarrow x=1\pm\sqrt{5}\)
3.
ĐK: \(x\ge-9\)
\(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)
\(\Leftrightarrow\left(x^2-x+1\right)\left(\sqrt{x+9}+x^2-9\right)=0\)
\(\Leftrightarrow\sqrt{x+9}+x^2-9=0\left(1\right)\)
Đặt \(\sqrt{x+9}=t\left(t\ge0\right)\Rightarrow9=t^2-x\)
\(\left(1\right)\Leftrightarrow t+x^2+x-t^2=0\)
\(\Leftrightarrow\left(x+t\right)\left(x-t+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-t\\x=t-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{x+9}\\x=\sqrt{x+9}-1\end{matrix}\right.\)
\(\Leftrightarrow...\)

d. \(\sqrt{9x^2+12x+4}=4\)
<=> \(\sqrt{\left(3x+2\right)^2}=4\)
<=> \(|3x+2|=4\)
<=> \(\left[{}\begin{matrix}3x+2=4\\3x+2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=2\\3x=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-2\end{matrix}\right.\)
c: Ta có: \(\dfrac{5\sqrt{x}-2}{8\sqrt{x}+2.5}=\dfrac{2}{7}\)
\(\Leftrightarrow35\sqrt{x}-14=16\sqrt{x}+5\)
\(\Leftrightarrow x=1\)

a:Sửa đề: \(\dfrac{3}{5x-1}+\dfrac{2}{3-x}=\dfrac{4}{\left(1-5x\right)\left(x-3\right)}\)
=>3x-9-10x+2=-4
=>-7x-7=-4
=>-7x=3
=>x=-3/7
b: =>\(\dfrac{5-x}{4x\left(x-2\right)}+\dfrac{7}{8x}=\dfrac{x-1}{2x\left(x-2\right)}+\dfrac{1}{8\left(x-2\right)}\)
=>\(2\left(5-x\right)+7\left(x-2\right)=4\left(x-1\right)+x\)
=>10-2x+7x-14=4x-4+x
=>5x-4=5x-4
=>0x=0(luôn đúng)
Vậy: S=R\{0;2}

24:
\(\Leftrightarrow\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}+\dfrac{1}{\left(x+4\right)\left(x+5\right)}+\dfrac{1}{\left(x+5\right)\left(x+6\right)}=\dfrac{1}{8}\)
\(\Leftrightarrow\dfrac{1}{x+2}-\dfrac{1}{x+6}=\dfrac{1}{8}\)
\(\Leftrightarrow\left(x+2\right)\left(x+6\right)=8\left(x+6\right)-8\left(x+2\right)\)
\(\Leftrightarrow x^2+8x+12=8x+48-8x-16=32\)
=>(x+10)(x-2)=0
=>x=-10 hoặc x=2
25: \(\Leftrightarrow\dfrac{\left(x+1\right)^2+1}{x+1}+\dfrac{\left(x+4\right)^2+4}{x+4}=\dfrac{\left(x+2\right)^2+2}{x+2}+\dfrac{\left(x+3\right)^2+3}{x+3}\)
\(\Leftrightarrow x+1+\dfrac{1}{x+1}+x+4+\dfrac{4}{x+4}=x+2+\dfrac{2}{x+2}+x+3+\dfrac{3}{x+3}\)
\(\Leftrightarrow\dfrac{1}{x+1}+\dfrac{4}{x+4}=\dfrac{2}{x+2}+\dfrac{3}{x+3}\)
\(\Leftrightarrow x+5=0\)
hay x=-5

1) điều kiện xác định : \(x\notin\left\{-1;-3;-5;-7\right\}\)
ta có : \(\dfrac{1}{x^2+4x+3}+\dfrac{1}{x^2+8x+15}+\dfrac{1}{x^2+12x+35}=\dfrac{1}{9}\)
\(\Leftrightarrow\dfrac{1}{\left(x+1\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+5\right)}+\dfrac{1}{\left(x+5\right)\left(x+7\right)}=\dfrac{1}{9}\) \(\Leftrightarrow\dfrac{\left(x+5\right)\left(x+7\right)+\left(x+1\right)\left(x+7\right)+\left(x+1\right)\left(x+3\right)}{\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)}=\dfrac{1}{9}\)\(\Leftrightarrow\dfrac{x^2+12x+35+x^2+8x+7+x^2+4x+3}{\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)}=\dfrac{1}{9}\)
\(\Leftrightarrow\dfrac{3x^2+24x+45}{\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)}=\dfrac{1}{9}\)
\(\Leftrightarrow9\left(3x^2+24x+45\right)=\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)\)
\(\Leftrightarrow27\left(x^2+8x+15\right)=\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)\)
\(\Leftrightarrow27\left(x+3\right)\left(x+5\right)=\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)\)
\(\Leftrightarrow27=\left(x+1\right)\left(x+7\right)\) ( vì điều kiện xác định )
\(\Leftrightarrow27=x^2+8x+7\Leftrightarrow x^2+8x-20=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+10\right)=0\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+10=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-10\end{matrix}\right.\left(tmđk\right)\)
vậy \(x=2\) hoặc \(x=-10\)


g: =>12x+1>=36x+12-24x-3
=>12x+1>=12x+9(loại)
h: =>6(x-1)+4(2-x)<=3(3x-3)
=>6x-6+8-4x<=9x-9
=>2x+2<=9x-9
=>-7x<=-11
=>x>=11/7
i: =>4x^2-12x+9>4x^2-3x
=>-12x+9>-3x
=>-9x>-9
=>x<1
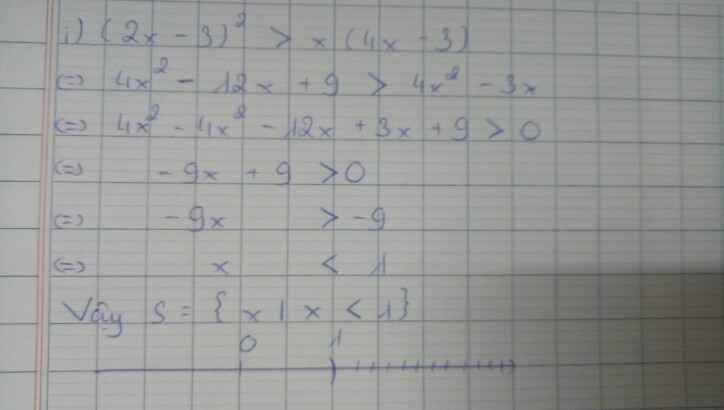

\(\Leftrightarrow\dfrac{2}{\left(x+1\right)\left(x+3\right)}+\dfrac{2}{\left(x+3\right)\left(x+5\right)}+\dfrac{2}{\left(x+5\right)\left(x+7\right)}+\dfrac{2}{\left(x+7\right)\left(x+9\right)}=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+5}+\dfrac{1}{x+5}-\dfrac{1}{x+7}+\dfrac{1}{x+7}-\dfrac{1}{x+9}=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+9}=\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{x+9-x-1}{\left(x+1\right)\left(x+9\right)}=\dfrac{2}{5}\)
=>2(x+1)(x+9)=5*8=40
=>x^2+9x+9=20
=>x^2+9x-11=0
hay \(x=\dfrac{-9\pm5\sqrt{5}}{2}\)
=>x^2+9x