Cho hình vuông ABCD, O là giao điểm của hai đường chéo. Gọi E là trung điểm của OC, F là trung điểm của AB. CMR
a, ED=EF
b,DEF=90 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
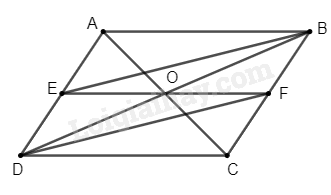
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)
Suy ra \(AE = ED = BF = FC\)
Xét tứ giác \(EBFD\) ta có:
\(ED = FB\) (cmt)
\(ED\) // \(BF\) (do \(AD\) // \(BC\))
Suy ra \(EDFB\) là hình bình hành
b) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Mà \(DEBF\) là hình bình hành (gt)
Suy ra \(O\) cũng là trung điểm của \(EF\)
Suy ra \(E\), \(O\), \(F\) thẳng hàng
22 tháng 10 2021
Bài 2:
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật
8 tháng 2 2023
Xét ΔOAB có E,F lần lượtlà trung điểm của OA,OB
nên EF là đường trung bình
=>EF//ABvà EF=AB/2
Xét ΔOCD có
H,G lần lượt là trung điểm của OD,OC
nên HG là đường trung bình
=>HG//DC và GH=DC/2
=>EF//GH và EF=GH
Xét ΔOAD có OH/OD=OE/OA
nên EH//AD
=>EH vuông góc AB
=>EH vuông góc EF
Xét tứ giác EHGF có
EF//GH
EF=GH
EH vuông góc EF
=>EHGF là hình chữ nhật
7 tháng 8 2023
a: Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
=>ΔABC=ΔBAD
=>góc OBA=góc OAB
=>OA=OB
OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD
b: Xét ΔEDC có AB//DC
nên EA/AD=EB/BC
mà AD=BC
nên EA=EB
EA+AD=ED
EB+BC=EC
mà EA=EB và AD=BC
nên ED=EC
EA=EB
OA=OB
=>EO là trung trực của AB
EC=ED
OC=OD
=>EO là trung trực của CD
các bn giải giúp mik vs
mình đang cần gấp