cho x,y là 2 số thực thỏa mãn x+y-xy=155 và x2+y2=325
tính giá trị của \(\left|x^3-y^3\right|\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^2+y^2=325\)
<=> \(\left(x+y\right)^2-2xy=325\)
Đặt: \(x+y=a;\)\(xy=b\)Khi đó ta có:
\(a-b=155\) (1)
và \(a^2-2b=325\)
Từ (1) ta có: \(b=a-155\) thay vào (2) ta được:
\(a^2-2\left(a-155\right)=325\)
giải ra tìm được: \(\orbr{\begin{cases}a=5\\a=-3\end{cases}}\) => \(\orbr{\begin{cases}a=5;b=-150\\a=-3;b=-158\end{cases}}\)
TH1: \(\hept{\begin{cases}a=5\\b=-150\end{cases}}\) ,=> \(\hept{\begin{cases}x+y=5\\xy=-150\end{cases}}\)
\(x^2+y^2=325\)
<=> \(\left(x-y\right)^2+2xy=325\)
<=> \(\left(x-y\right)^2=325-2xy=625\)
<=> \(\left|x-y\right|=25\)
=> \(\left|x^3-y^3\right|=\left|\left(x-y\right)\left(x^2+y^2+xy\right)\right|=\left|x-y\right|\left(x^2+y^2+xy\right)=4375\)
TH2: bn tự lm tiếp nhé

Ta có ( x + y ) 2 = x 2 + y 2 + 2 x y = 4 − 2 3 = ( 3 − 1 ) 2 ⇒ x + y = 3 − 1.
Suy ra P = x + y = 3 − 1 k h i x + y ≥ 0 1 − 3 k h i x + y < 0 .

Ta có \(x^2+y^2+xy+x=y-1\)
\(\Leftrightarrow2x^2+2y^2+2xy+2x-2y+2=0\)
\(\Leftrightarrow\left(x+y\right)^2+\left(x+1\right)^2+\left(y-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=0\\x+1=0\\y-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
\(\Rightarrow B=\left(-1+1-1\right)^{2023}\) \(=\left(-1\right)^{2023}\) \(=-1\)

Đáp án D
Phương pháp giải:
Đặt ẩn phụ, đưa về hàm một biến, dựa vào giả thiết để tìm điều kiện của biến
Lời giải:
Từ giả thiết chia cả 2 vế cho x2y2 ta được : 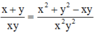
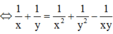
Đặt 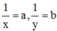 ta có
ta có ![]()
Khi đó ![]()
![]()
Ta có ![]() mà
mà 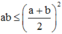
nên ![]()
![]()
![]()
Dấu đẳng thức xảy ra khi 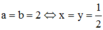 . Vậy Mmax = 16
. Vậy Mmax = 16

Đặt \(x+y=a\Leftrightarrow a-4=x+y-4\)
\(x^3+y^3-6\left(x^2+y^2\right)+13\left(x+y\right)-20=0\\ \Leftrightarrow\left(x+y\right)^3-6\left(x+y\right)^2+13\left(x+y\right)-20-3xy\left(x+y\right)+12xy=0\\ \Leftrightarrow a^3-6a^2+13a-20-3xy\left(x+y-4\right)=0\\ \Leftrightarrow a^3-4a^2-2a^2+8a+5a-20-3xy\left(a-4\right)=0\\ \Leftrightarrow\left(a-4\right)\left(a^2-2a+5\right)-3xy\left(a-4\right)=0\\ \Leftrightarrow\left(a-4\right)\left(a^2-2a+5-3xy\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=4\\a^2-2a+5-3xy=0\left(vô.n_0\right)\end{matrix}\right.\\ \Leftrightarrow x+y=4\)
\(\Leftrightarrow A=x^3+y^3+12xy=\left(x+y\right)^3-3xy\left(x+y\right)+12xy\\ A=4^3-3xy\left(x+y-4\right)=64-0=64\)

Đáp án D
Cho x,y > 0 thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( 2 + x y ) ⇔ 2 ( x + y ) 2 - ( 2 + x y ) ( x + y ) - 3 x y = 0 (*)
Đặt x + y = u x y = v ta đc PT bậc II: 2 u 2 - ( v + 2 ) u - 3 = 0 gải ra ta được u = v + 2 + v 2 + 28 v + 4 4
Ta có P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 ) = 4 ( x y + y x ) 3 - 9 ( x y + y x ) 2 - 12 ( x y + y x ) + 18 , đặt t = ( x y + y x ) , ( t ≥ 2 ) ⇒ P = 4 t 3 - 9 t 2 - 12 t + 18 ; P ' = 6 ( 2 t 2 - 3 t + 2 ) ≥ 0 với ∀ t ≥ 2 ⇒ M i n P = P ( t 0 ) trong đó t 0 = m i n t = m i n ( x y + y x ) với x,y thỏa mãn điều kiện (*).
Ta có :
t = ( x y + y x ) = ( x + y ) 2 x y - 2 = u 2 v - 2 = ( v + 2 + v 2 + 28 v + 4 ) 2 16 v - 2 = 1 16 ( v + 2 v + v + 4 v + 28 ) 2 - 2 ≥ 1 16 ( 2 2 + 32 ) 2 - 2 = 5 2
Vậy m i n P = P ( 5 2 ) = 4 . ( 5 2 ) 2 - 9 ( 5 2 ) 2 - 12 . 5 2 + 18 = - 23 4
Lớp 8 chưa sử dụng được phương pháp nghiệm pt bậc 2 đúng ko bạn? Vậy chỉ còn cách phân tích đa thức thành nhân tử thôi
\(x^2+y^2=325\Rightarrow\left(x+y\right)^2-2xy=325\) , đặt \(x+y=a\) và \(xy=b\)
Từ pt đầu ta có \(a-b=155\Rightarrow b=a-155\) , thay vào pt sau:
\(a^2-2b=325\Rightarrow a^2-2\left(a-155\right)=325\Rightarrow a^2-2a-15=0\)
\(\Rightarrow\left(a-1\right)^2-16=0\Rightarrow\left(a-5\right)\left(a+3\right)=0\) \(\Rightarrow a=5;b=-150\) hoặc \(a=-3;b=-158\)
TH1: \(\left\{{}\begin{matrix}x+y=5\\x.y=-150\end{matrix}\right.\), ta biến đổi
\(x^2+y^2=325\Leftrightarrow\left(x-y\right)^2+2xy=325\Leftrightarrow\left(x-y\right)^2=325-2xy=625\)
\(\Rightarrow\left|x-y\right|=25\)
\(\Rightarrow\left|x^3-y^3\right|=\left|\left(x-y\right)\left(x^2+y^2+xy\right)\right|=\left|x-y\right|\left(x^2+y^2+xy\right)=25.\left(325-150\right)=4375\)
TH2: \(x.y=-158\Rightarrow\left(x-y\right)^2=325-2xy=641\Rightarrow\left|x-y\right|=\sqrt{641}\)
\(\Rightarrow\left|x^3-y^3\right|=\left|x-y\right|\left(x^2+y^2+xy\right)=\sqrt{641}\left(325-158\right)=167\sqrt{641}\)