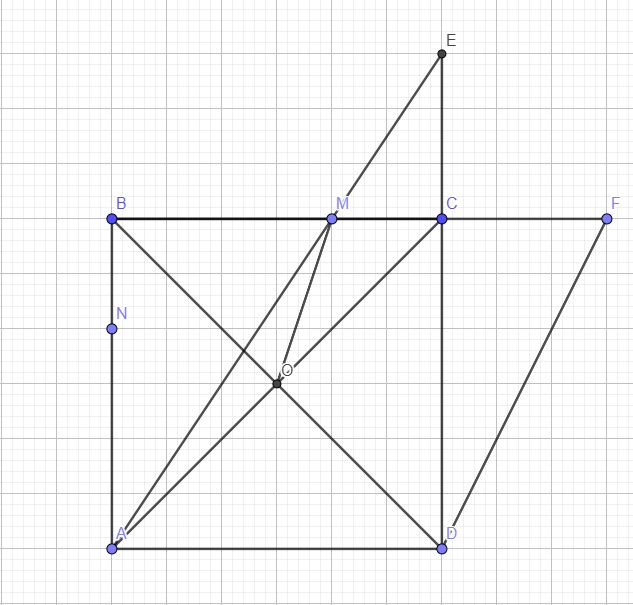
Cho hình vuông ABCD có góc B = góc D= 90 độ và AB=AD. Trên cạnh BC lấy điểm M và trên cạnh CD lấy điểm N sao cho AM vuông góc BN. Gọi H là giao điểm thẳng AM và BN; gọi K là giao điểm của đoạn thẳng AN và BM. Chứng minh rằng AH.AM=AK.AN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 2 2023
Xét ΔIAB và ΔICD có
góc IAB=góc ICD
goc AIB=góc CID
=>ΔIAB đồng dạng với ΔICD
=>IB/ID=AB/CD=BM/MC
=>IM//DC
=>IM vuông góc AD
1 tháng 4 2023
Xét ΔBAN và ΔADE có
góc BAN=góc ADE
AB=AD
góc ABN=góc DAE
=>ΔBAN=ΔADE
=>AN=DE=AM
mà AB=CD
nên BM=CE
mà BM//CE
nên BMEC là hình bình hành
mà góc B=90 độ
nên BMEC là hình chữ nhật
Gọi O là giao của BE và CM
=>OB=OE=OC=OM
ΔBHE vuông tạiH có HO là trung tuyến
nên HO=OB=OE
=>HO=OC=OM
=>ΔMHC vuông tại H
=>góc MHC=90 độ
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1
a.
DO ABCD là hình vuông \(\Rightarrow\widehat{ACD}=45^0\)
\(\Rightarrow\widehat{ACD}=\widehat{EBN}\)
Mà \(\widehat{ACD}\) và \(\widehat{EBN}\) cùng chắn EN
\(\Rightarrow\) Tứ giác BENC nội tiếp
\(\Rightarrow\widehat{BEN}+\widehat{BCN}=180^0\)
\(\Rightarrow\widehat{BEN}=180^0-\widehat{BCN}=180^0-90^0=90^0\)
\(\Rightarrow NE\perp BM\) tại E
b.
Tương tự ta có tứ giác ABFM nội tiếp (\(\widehat{MAF}=\widehat{MBF}=45^0\) cùng chắn MF)
\(\Rightarrow\widehat{BFM}+\widehat{BAM}=180^0\)
\(\Rightarrow\widehat{BFM}=90^0\Rightarrow MF\perp BN\)
\(\Rightarrow I\) là trực tâm của tam giác BMN
\(\Rightarrow BI\perp MN\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1
c.
Gọi H là giao điểm BI và MN
Do E và F cùng nhìn MN dưới 1 góc vuông
\(\Rightarrow\) Tứ giác EFMN nội tiếp
\(\Rightarrow\widehat{EMN}+\widehat{EFN}=180^0\)
Mà \(\widehat{EFN}+\widehat{EFB}=180^0\)
\(\Rightarrow\widehat{EMN}=\widehat{EFB}\)
Lại có tứ giác ABFM nội tiếp (A và F cùng nhìn BM dưới 1 góc vuông)
\(\Rightarrow\widehat{EFB}=\widehat{AMB}\) (cùng chắn AB)
\(\Rightarrow\widehat{EMN}=\widehat{AMB}\)
\(\Rightarrow\Delta_VAMB=\Delta_VHMB\left(ch-gn\right)\)
\(\Rightarrow AM=HM\)
Đồng thời suy ra \(AB=BH\Rightarrow BH=BC\) (do AB=BC)
Theo Pitago: \(\left\{{}\begin{matrix}HN=\sqrt{BN^2-BH^2}\\CN=\sqrt{BN^2-BC^2}\end{matrix}\right.\) \(\Rightarrow CN=HN\)
\(\Rightarrow AM+CN=MH+NH=MN\)
\(\Rightarrow MD+DN+MN=MD+DN+AM+CN=AD+CD=2a\)
Pitago: \(MN^2=DM^2+DN^2\ge\dfrac{1}{2}\left(DM+DN\right)^2\Rightarrow MN\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a-\left(DM+DN\right)\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a\ge\left(\dfrac{2+\sqrt{2}}{2}\right)\left(DM+DN\right)\ge\left(2+\sqrt{2}\right).\sqrt{DM.DN}\)
\(\Rightarrow DM.DN\le\left(6-4\sqrt{2}\right)a^2\)
\(\Rightarrow S_{MDN}=\dfrac{1}{2}DM.DN\le\left(3-2\sqrt{2}\right)a^2\)
Dấu "=" xảy ra khi \(DM=DN=\left(\sqrt{6}-\sqrt{2}\right)a\)
11 tháng 10 2023
a: XétΔMAD vuông tại A và ΔNBA vuông tại B có
MA=NB
AD=BA
Do đó: ΔMAD=ΔNBA
=>DM=AN và \(\widehat{AMD}=\widehat{BNA}\)
=>\(\widehat{AMD}+\widehat{MAN}=90^0\)
=>DM vuông góc AN
b: AM+MB=AB
BN+NC=BC
mà AM=BN và AB=BC
nên MB=NC
Xét ΔMBC vuông tại B và ΔNCD vuông tại C có
MB=NC
BC=CD
Do đó: ΔMBC=ΔNCD
=>\(\widehat{BMC}=\widehat{CND}\)
=>\(\widehat{CND}+\widehat{NCM}=90^0\)
=>DN vuông góc MC
Xét ΔDMN có
CM,NA là đường cao
CM cắt NA tại X
Do đó: X là trực tâm
=>DX vuông góc MN
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
Đặt cạnh hình vuông là a, ta có \(BD=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow BO.BD=a^2\)
Xét 2 tam giác vuông AED và MAB có:
\(\left\{{}\begin{matrix}\widehat{ADE}=\widehat{MBA}=90^0\\\widehat{AED}=\widehat{MAB}\left(slt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{BM}=\dfrac{ED}{AB}\Rightarrow BM.ED=AD.AB=a^2\)
\(\Rightarrow BM.ED=BO.BD\)
Mà \(ED=BF\) (do \(BC=CD\) và \(CE=CF\))
\(\Rightarrow BM.BF=BO.BD\Rightarrow\dfrac{BM}{BD}=\dfrac{BO}{BF}\)
Xét hai tam giác BOM và BFD có:
\(\left\{{}\begin{matrix}\dfrac{BM}{BD}=\dfrac{BO}{BF}\\\widehat{OBM}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOM\sim\Delta BFD\left(c.g.c\right)\)
